CF1981F Turtle and Paths on a Tree

在这个问题中，注意 $\text{MEX}$ 的不寻常定义。 Piggy 给了 Turtle 一棵二叉树，有 $n$ 个顶点和一个序列 $a_1, a_2, \ldots, a_n$ 。这棵二叉树以顶点 $1$ 为根。 如果一组路径 $P={(x_i, y_i)}$ 在树中正好覆盖每条边一次，那么 Turtle 就认为这组路径是好的。注意，好的路径集可以多次覆盖一个顶点。 Turtle 将一组路径的值定义为 $\sum\limits_{(x,y)\in P} f(x,y)$，其中 $f(x,y)$ 表示从路径 $x$ 到 $y$ 的简单路径上所有顶点的 $\text{MEX}$ 值（包括起始顶点 $x$ 和结束顶点 $y$）。 Turtle 想知道所有好的路径集中的最小值。请帮助他计算答案！

每个测试包含多个测试用例。第一行包含测试用例数 $t$ （$1\leq t \leq 10^4$）。接下来是每个测试用例的描述。 每个测试用例的第一行包含一个整数 $n$ （$2\leq n \leq 2.5 \times 10^4$）。这是树中顶点的数量。 每个测试用例的第二行包含 $n$ 个整数 $a_1, a_2, \ldots, a_n$ （$1 \leq a_i \leq 10^9$） — 序列 $a$ 的元素。 每个测试用例的第三行包含 $n-1$ 个整数 $p_2, p_3, \ldots, p_n$ （$1 \leq p_i < i$） — 树中每个顶点的父节点。 输入中的额外约束条件：给定的树是二叉树，即每个非叶节点最多有 $2$ 个儿子。 保证所有测试用例中 $n$ 的总和不超过 $10^5$。

对于每个测试用例，输出一个整数 — 所有好路径集中的最小值。

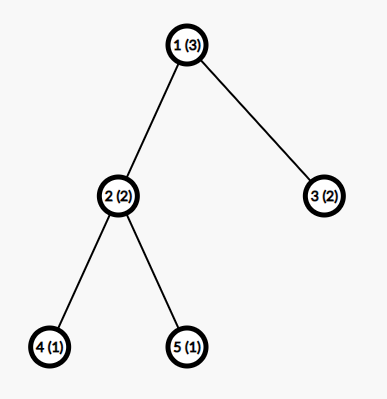In the first test case, the tree is as follows. The number in brackets denotes the weight of the vertex: The good set of paths with the minimum value is $ \{(2, 3), (4, 5)\} $ . Note that in this test case $ \{(4, 5)\} $ and $ \{(3, 4), (4, 5)\} $ are not good sets of paths because each edge should be covered exactly once. In the second test case, the tree is as follows: The set of good paths with the minimum value is $ \{(1, 2), (1, 3), (4, 5)\} $ . 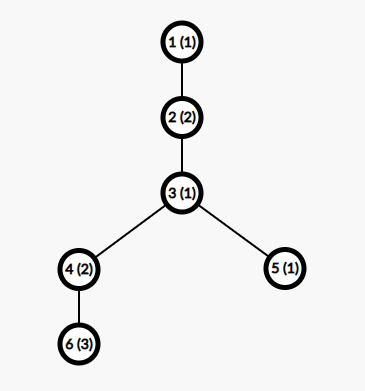In the third test case, the tree is as follows: The set of good paths with the minimum value is $ \{(1, 6), (3, 5)\} $ .