CF1981F Turtle and Paths on a Tree

Note the unusual definition of $ \text{MEX} $ in this problem. Piggy gave Turtle a binary tree $ ^{\dagger} $ with $ n $ vertices and a sequence $ a_1, a_2, \ldots, a_n $ on his birthday. The binary tree is rooted at vertex $ 1 $ . If a set of paths $ P = \{(x_i, y_i)\} $ in the tree covers each edge exactly once, then Turtle will think that the set of paths is good. Note that a good set of paths can cover a vertex twice or more. Turtle defines the value of a set of paths as $ \sum\limits_{(x, y) \in P} f(x, y) $ , where $ f(x, y) $ denotes the $ \text{MEX}^{\ddagger} $ of all $ a_u $ such that vertex $ u $ is on the simple path from $ x $ to $ y $ in the tree (including the starting vertex $ x $ and the ending vertex $ y $ ). Turtle wonders the minimum value over all good sets of paths. Please help him calculate the answer! $ ^{\dagger} $ A binary tree is a tree where every non-leaf vertex has at most $ 2 $ sons. $ ^{\ddagger}\text{MEX} $ of a collection of integers $ c_1, c_2, \ldots, c_k $ is defined as the smallest positive integer $ x $ which does not occur in the collection $ c $ . For example, $ \text{MEX} $ of $ [3, 3, 1, 4] $ is $ 2 $ , $ \text{MEX} $ of $ [2, 3] $ is $ 1 $ .

Each test contains multiple test cases. The first line contains the number of test cases $ t $ ( $ 1 \le t \le 10^4 $ ). The description of the test cases follows. The first line of each test case contains a single integer $ n $ ( $ 2 \le n \le 2.5 \cdot 10^4 $ ) — the number of vertices in the tree. The second line of each test case contains $ n $ integers $ a_1, a_2, \ldots, a_n $ ( $ 1 \le a_i \le 10^9 $ ) — the elements of the sequence $ a $ . The third line of each test case contains $ n - 1 $ integers $ p_2, p_3, \ldots, p_n $ ( $ 1 \le p_i < i $ ) — the parent of each vertex in the tree. Additional constraint on the input: the given tree is a binary tree, that is, every non-leaf vertex has at most $ 2 $ sons. It is guaranteed that the sum of $ n $ over all test cases does not exceed $ 10^5 $ .

For each test case, output a single integer — the minimum value over all good sets of paths.

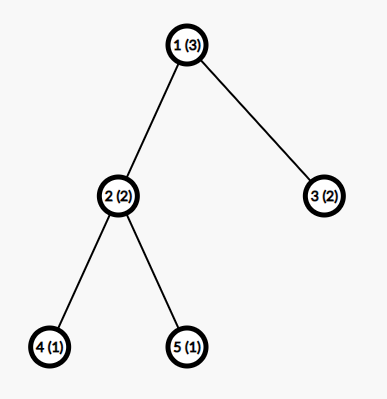In the first test case, the tree is as follows. The number in brackets denotes the weight of the vertex: The good set of paths with the minimum value is $ \{(2, 3), (4, 5)\} $ . Note that in this test case $ \{(4, 5)\} $ and $ \{(3, 4), (4, 5)\} $ are not good sets of paths because each edge should be covered exactly once. In the second test case, the tree is as follows: The set of good paths with the minimum value is $ \{(1, 2), (1, 3), (4, 5)\} $ . 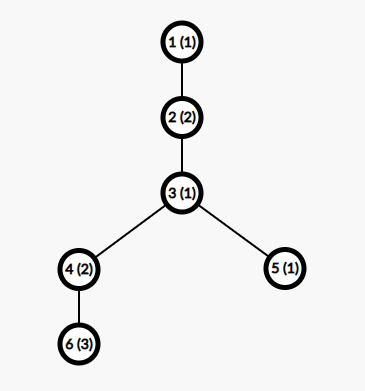In the third test case, the tree is as follows: The set of good paths with the minimum value is $ \{(1, 6), (3, 5)\} $ .