CF1982D Beauty of the mountains
题目描述
Nikita 喜爱山脉,终于决定前往 Berlyand 山脉旅行!山脉太美了,于是 Nikita 决定把它画在地图上。地图是一个 $n$ 行 $m$ 列的表格,每个格子里有一个非负整数,表示该处山的高度。
他还注意到山脉有两种类型:
- 有雪顶的山。
- 没有雪顶的山。
Nikita 是个非常务实的人。他希望有雪顶的山的高度之和等于没有雪顶的山的高度之和。他已经和 Berlyand 市长 Polikarp Polikarpovich 协商好,可以对地形进行改造。
Nikita 可以对任意 $k \times k$ 的子矩阵进行如下操作:他可以给该区域内所有山的高度加上一个整数常数 $c$,但山的类型不会改变。每次操作可以独立选择 $c$,且 $c$ 可以为负数。
在进行操作前,Nikita 想知道是否有可能使两类山的高度和相等,或者这是不可能的。无论付出什么代价都可以,即使山变成了峡谷,高度为负也没关系。
如果地图上只有一种类型的山,则另一种类型的山的高度和视为 $0$。
输入格式
每组测试数据包含若干组测试用例。第一行包含一个整数 $t$($1 \le t \le 10^{4}$),表示测试用例的组数。接下来是每组测试用例的描述。
每组测试用例的第一行包含三个整数 $n, m, k$($1 \le n, m \le 500, 1 \le k \le \min(n, m)$)。
接下来的 $n$ 行,每行包含 $m$ 个整数 $a_{ij}$($0 \le a_{ij} \le 10^{9}$),表示初始的山高。
接下来的 $n$ 行,每行是一个长度为 $m$ 的二进制字符串,表示山的类型,'0' 表示有雪顶,'1' 表示无雪顶。
保证所有测试用例中 $n \cdot m$ 的总和不超过 $250\,000$。
输出格式
对于每组测试用例,如果可以使两类山的高度和相等,输出 "YES"(不带引号),否则输出 "NO"(不带引号)。输出大小写不敏感(如 "yEs"、"yes"、"Yes"、"YES" 都视为正确)。
说明/提示
第一组测试用例的山脉数组如下:
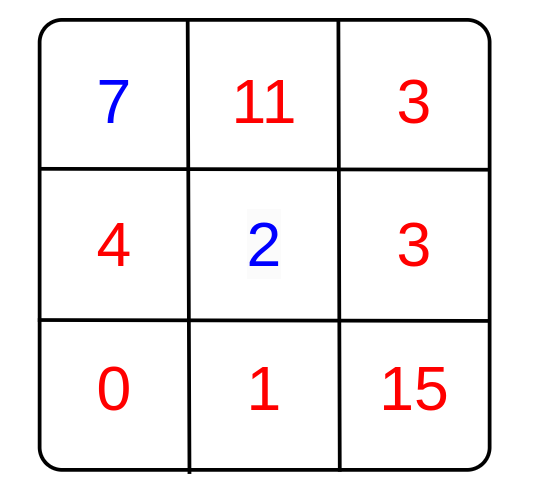
初始时,有雪顶的山的高度和为 $11 + 3 + 4 + 3 + 0 + 1 + 15 = 37$,无雪顶的山的高度和为 $7 + 2 = 9$。
为了使这两个和相等,我们可以进行两次操作:
第一次操作:
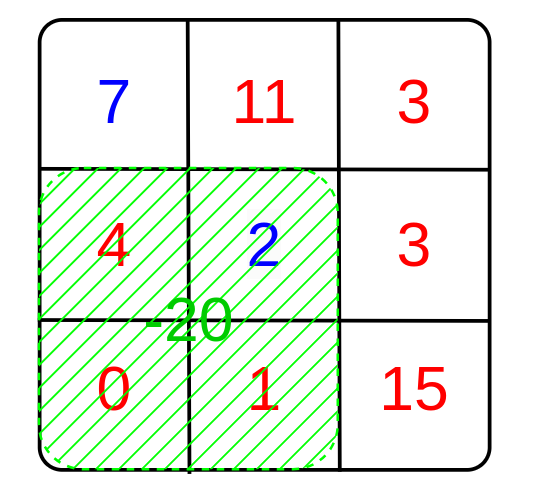
注意常数 $c$ 可以为负数。
第一次操作后,山脉数组变为:
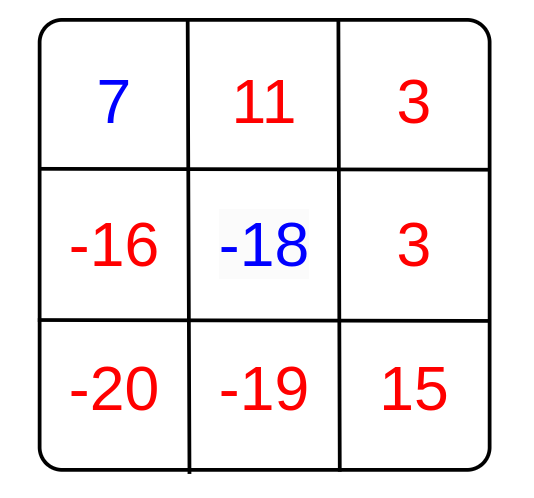
第二次操作:
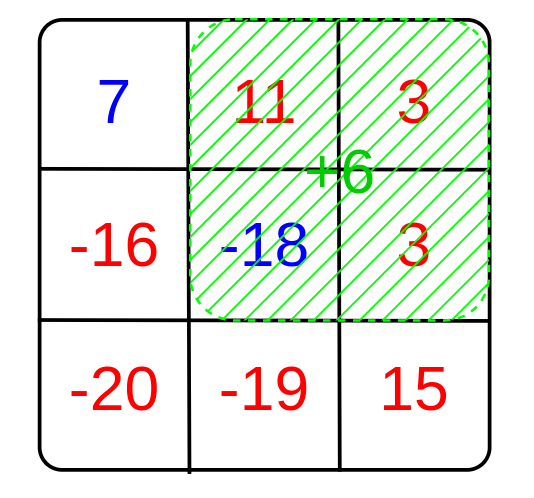
最终,山脉数组变为:
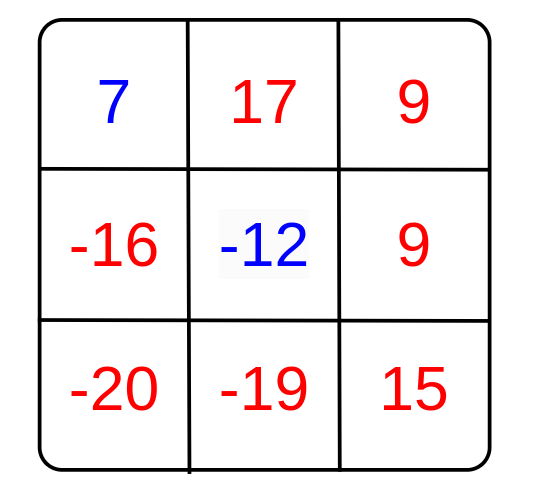
此时有雪顶的山的高度和为 $17 + 9 + 9 - 16 - 20 - 19 + 15 = -5$,无雪顶的山的高度和为 $7 - 12 = -5$,因此答案为 YES。
由 ChatGPT 4.1 翻译