CF1984E Shuffle

两只饥饿的小熊猫 Oscar 和 Lura 有一棵包含 $n$ 个节点的树 $T$。它们打算对整棵树 $T$ 执行一次如下的洗牌操作。通过这个洗牌操作，它们会用原树的节点构造出一棵新树。 1. 从原树 $T$ 中任选一个节点 $V$，以 $V$ 作为根节点，创建一棵新树 $T_2$。 2. 将 $V$ 从 $T$ 中移除，此时原树会被分裂成一个或多个子树（如果 $V$ 是 $T$ 唯一的节点，则不会有子树）。 3. 对每棵子树重复上述操作（同样任选一个节点作为根），然后将所有洗牌后子树的根节点连接回 $V$，完成新树 $T_2$ 的构建。 经过上述操作后，Oscar 和 Lura 得到了一棵新树 $T_2$。它们只能吃叶子节点，而且非常饥饿，请你帮忙计算：在对整棵树恰好执行一次洗牌操作后，所能获得的最大叶子节点数是多少。 注意，叶子节点指的是度为 $1$ 的所有节点。因此，如果根节点只有一个子节点，也可以被视为叶子节点。

第一行包含一个整数 $t$（$1 \leq t \leq 10^4$），表示测试用例的数量。 每个测试用例的第一行包含一个整数 $n$（$2 \leq n \leq 2 \times 10^5$），表示原树 $T$ 的节点数。 接下来的 $n-1$ 行，每行包含两个整数 $u$ 和 $v$（$1 \leq u, v \leq n$），表示原树 $T$ 中的一条边。所给边集保证构成一棵树。 所有测试用例中 $n$ 的总和不超过 $3 \times 10^5$。

对于每个测试用例，输出一个整数，表示经过一次洗牌操作后，所能获得的最大叶子节点数。

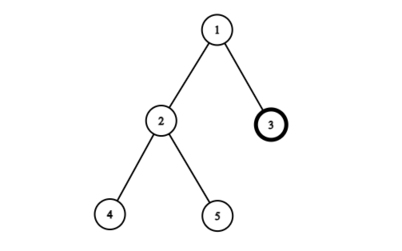
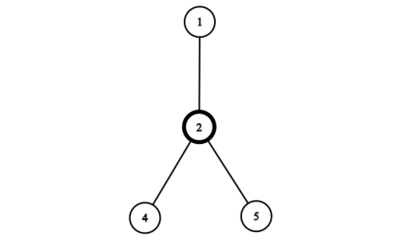
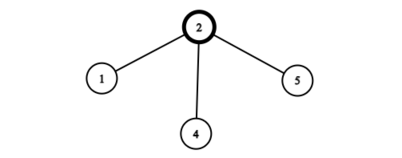
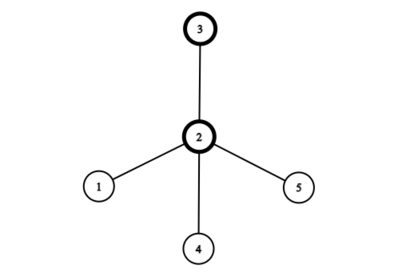
在第一个测试用例中，可以证明最大叶子节点数为 $4$。实现方法如下：首先选择节点 $3$ 作为新树的根节点。  接下来只剩下一个子树，我们可以选择节点 $2$ 作为该子树的新根。  这样会使剩下的 $3$ 个节点都变成叶子节点，将它们连接回新根后，洗牌后的子树如下：  最后将洗牌后的子树连接回新树的根节点，最终树有 $4$ 个叶子节点（包括根节点），如下所示：  在第二个测试用例中，原树是一条包含五个节点的链。可以证明经过一次洗牌后，最大叶子节点数为 $3$。我们可以先选择节点 $2$ 作为根节点，这样节点 $1$ 会变成叶子节点。然后在右侧选择节点 $4$，这样节点 $3$ 和 $5$ 也会变成叶子节点。 第三个测试用例是一颗有六个节点的星形树。叶子节点数无法增加，因此答案为 $5$（如果我们以原根节点开始洗牌）。 由 ChatGPT 4.1 翻译