CF1984H Tower Capturing

有 $n$ 个塔，分别位于 $n$ 个不同的点 $(x_1, y_1), (x_2, y_2), \ldots, (x_n, y_n)$，保证没有三点共线，也没有四点共圆。最开始，你拥有 $(x_1, y_1)$ 和 $(x_2, y_2)$ 这两个塔，你的目标是占领所有的塔。为此，你可以进行如下操作任意次： - 选择你已经拥有的两个塔 $P$ 和 $Q$，以及一个你尚未拥有的塔 $R$，要求经过 $P$、$Q$、$R$ 的圆能够包含所有 $n$ 个塔在其内部或边界上。 - 然后，你可以占领在三角形 $\triangle PQR$ 内部或边界上的所有塔，包括 $R$ 本身。 一次“攻击方案”是指一系列选择 $R$（$R_1, R_2, \ldots, R_k$）的操作，最终使你占领了所有的塔。注意，只有当某一步选择的 $R$ 不同时，两个攻击方案才被认为是不同的；如果选择的 $R$ 相同，但 $P$ 和 $Q$ 不同，则认为是同一个方案。请你计算最短长度的攻击方案的数量。如果无法占领所有塔，输出 $0$。 由于答案可能很大，请输出对 $998\,244\,353$ 取模后的结果。

第一行包含一个整数 $t$（$1 \leq t \leq 250$），表示测试用例的数量。 每个测试用例的第一行包含一个整数 $n$（$4 \leq n \leq 100$），表示塔的数量。 接下来的 $n$ 行，每行包含两个整数 $x_i$ 和 $y_i$（$-10^4 \leq x_i, y_i \leq 10^4$），表示第 $i$ 个塔的位置。最开始你拥有 $(x_1, y_1)$ 和 $(x_2, y_2)$ 这两个塔。 所有塔的位置均不相同，且没有三点共线，也没有四点共圆。 所有测试用例中 $n$ 的总和不超过 $1000$。

对于每个测试用例，输出一个整数，表示能够占领所有塔的最短攻击方案数量，对 $998\,244\,353$ 取模。

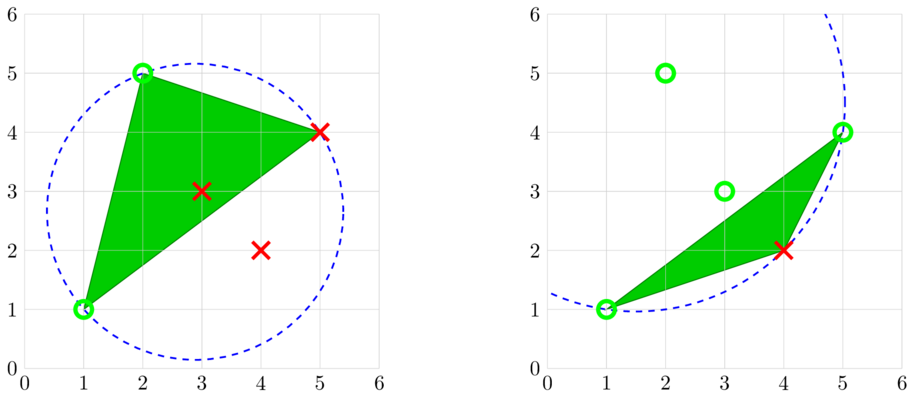
在第一个测试用例中，只有一种最短的攻击方案，如下图所示。  - 第一步，选择 $P=$塔 $1$，$Q=$塔 $2$，$R=$塔 $5$。经过这三座塔的圆包含了所有塔，因此塔 $3$ 和塔 $5$ 都被占领。 - 第二步，选择 $P=$塔 $5$，$Q=$塔 $1$，$R=$塔 $4$。经过这三座塔的圆包含了所有塔，因此塔 $4$ 被占领。 在第二个测试用例中，例如，位于 $(3, 10\,000)$ 的塔永远无法被占领。 由 ChatGPT 4.1 翻译