CF1984H Tower Capturing

There are $ n $ towers at $ n $ distinct points $ (x_1, y_1), (x_2, y_2), \ldots, (x_n, y_n) $ , such that no three are collinear and no four are concyclic. Initially, you own towers $ (x_1, y_1) $ and $ (x_2, y_2) $ , and you want to capture all of them. To do this, you can do the following operation any number of times: - Pick two towers $ P $ and $ Q $ you own and one tower $ R $ you don't own, such that the circle through $ P $ , $ Q $ , and $ R $ contains all $ n $ towers inside of it. - Afterwards, capture all towers in or on triangle $ \triangle PQR $ , including $ R $ itself. An attack plan is a series of choices of $ R $ ( $ R_1, R_2, \ldots, R_k $ ) using the above operations after which you capture all towers. Note that two attack plans are considered different only if they differ in their choice of $ R $ in some operation; in particular, two attack plans using the same choices of $ R $ but different choices of $ P $ and $ Q $ are considered the same.Count the number of attack plans of minimal length. Note that it might not be possible to capture all towers, in which case the answer is $ 0 $ . Since the answer may be large, output it modulo $ 998\,244\,353 $ .

The first line contains a single integer $ t $ ( $ 1 \leq t \leq 250 $ ) — the number of test cases. The first line of each test case contains a single integer $ n $ ( $ 4 \leq n \leq 100 $ ) — the number of towers. The $ i $ -th of the next $ n $ lines contains two integers $ x_i $ and $ y_i $ ( $ -10^4 \leq x_i, y_i \leq 10^4 $ ) — the location of the $ i $ -th tower. Initially, you own towers $ (x_1, y_1) $ and $ (x_2, y_2) $ . All towers are at distinct locations, no three towers are collinear, and no four towers are concyclic. The sum of $ n $ over all test cases does not exceed $ 1000 $ .

For each test case, output a single integer — the number of attack plans of minimal length after which you capture all towers, modulo $ 998\,244\,353 $ .

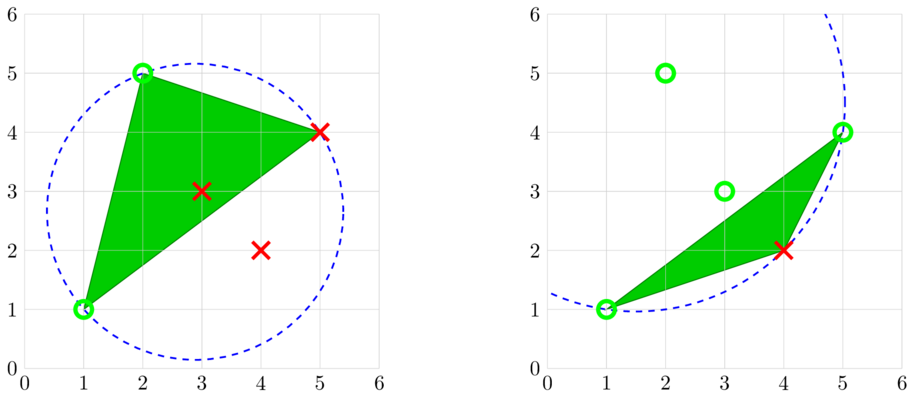In the first test case, there is only one possible attack plan of shortest length, shown below. - Use the operation with $ P = $ tower $ 1 $ , $ Q = $ tower $ 2 $ , and $ R = $ tower $ 5 $ . The circle through these three towers contains all towers inside of it, and as a result towers $ 3 $ and $ 5 $ are captured. - Use the operation with $ P = $ tower $ 5 $ , $ Q = $ tower $ 1 $ , and $ R = $ tower $ 4 $ . The circle through these three towers contains all towers inside of it, and as a result tower $ 4 $ is captured. In the second case, for example, you can never capture the tower at $ (3, 10\,000) $ .