CF1985E Secret Box

Ntarsis has a box $ B $ with side lengths $ x $ , $ y $ , and $ z $ . It lies in the 3D coordinate plane, extending from $ (0,0,0) $ to $ (x,y,z) $ . Ntarsis has a secret box $ S $ . He wants to choose its dimensions such that all side lengths are positive integers, and the volume of $ S $ is $ k $ . He can place $ S $ somewhere within $ B $ such that: - $ S $ is parallel to all axes. - every corner of $ S $ lies on an integer coordinate. $ S $ is magical, so when placed at an integer location inside $ B $ , it will not fall to the ground. Among all possible ways to choose the dimensions of $ S $ , determine the maximum number of distinct locations he can choose to place his secret box $ S $ inside $ B $ . Ntarsis does not rotate $ S $ once its side lengths are selected.

The first line consists of an integer $ t $ , the number of test cases ( $ 1 \leq t \leq 2000 $ ). The description of the test cases follows. The first and only line of each test case contains four integers $ x, y, z $ and $ k $ ( $ 1 \leq x, y, z \leq 2000 $ , $ 1 \leq k \leq x \cdot y \cdot z $ ). It is guaranteed the sum of all $ x $ , sum of all $ y $ , and sum of all $ z $ do not exceed $ 2000 $ over all test cases. Note that $ k $ may not fit in a standard 32-bit integer data type.

For each test case, output the answer as an integer on a new line. If there is no way to select the dimensions of $ S $ so it fits in $ B $ , output $ 0 $ .

For the first test case, it is optimal to choose $ S $ with side lengths $ 2 $ , $ 2 $ , and $ 2 $ , which has a volume of $ 2 \cdot 2 \cdot 2 = 8 $ . It can be shown there are $ 8 $ ways to put $ S $ inside $ B $ . The coordinate with the least $ x $ , $ y $ , and $ z $ values for each possible arrangement of $ S $ are: 1. $ (0, 0, 0) $ 2. $ (1, 0, 0) $ 3. $ (0, 1, 0) $ 4. $ (0, 0, 1) $ 5. $ (1, 0, 1) $ 6. $ (1, 1, 0) $ 7. $ (0, 1, 1) $ 8. 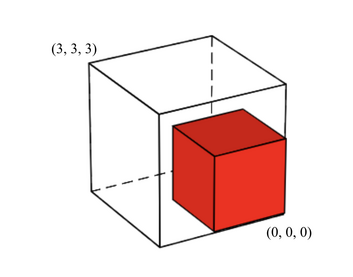$ (1, 1, 1) $ The arrangement of $ S $ with a coordinate of $ (0, 0, 0) $ is depicted below: For the second test case, $ S $ with side lengths $ 2 $ , $ 3 $ , and $ 3 $ are optimal.