CF1985E Secret Box
题目描述
Ntarsis 有一个边长分别为 $x$、$y$、$z$ 的盒子 $B$。它位于三维坐标系中,范围从 $(0,0,0)$ 到 $(x,y,z)$。
Ntarsis 有一个秘密盒子 $S$。他想选择 $S$ 的尺寸,使得所有边长都是正整数,并且 $S$ 的体积为 $k$。他可以将 $S$ 放在 $B$ 内的某个位置,使得:
- $S$ 与所有坐标轴平行。
- $S$ 的每个顶点都位于整数坐标点上。
$S$ 是魔法盒子,所以当它被放在 $B$ 内的整数位置时,不会掉到地上。
在所有可能选择 $S$ 的尺寸的方式中,求 Ntarsis 能将秘密盒子 $S$ 放在 $B$ 内的不同位置的最大数量。Ntarsis 选定 $S$ 的边长后,不会旋转 $S$。
输入格式
第一行包含一个整数 $t$,表示测试用例的数量($1 \leq t \leq 2000$)。接下来是每个测试用例的描述。
每个测试用例的第一行包含四个整数 $x, y, z, k$($1 \leq x, y, z \leq 2000$,$1 \leq k \leq x \cdot y \cdot z$)。
保证所有测试用例中 $x$ 的和、$y$ 的和、$z$ 的和均不超过 $2000$。
注意 $k$ 可能无法用标准的 32 位整数类型存储。
输出格式
对于每个测试用例,输出一个整数,表示答案。如果没有办法选择 $S$ 的尺寸使其能放入 $B$,输出 $0$。
说明/提示
对于第一个测试用例,最优选择 $S$ 的边长为 $2$、$2$、$2$,体积为 $2 \cdot 2 \cdot 2 = 8$。可以证明有 $8$ 种方式将 $S$ 放入 $B$。
每种可能的 $S$ 的左下角坐标为:
1. $(0, 0, 0)$
2. $(1, 0, 0)$
3. $(0, 1, 0)$
4. $(0, 0, 1)$
5. $(1, 0, 1)$
6. $(1, 1, 0)$
7. $(0, 1, 1)$
8. $(1, 1, 1)$
$S$ 放在 $(0, 0, 0)$ 时的示意图如下:
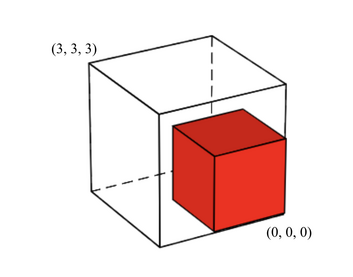
对于第二个测试用例,最优选择 $S$ 的边长为 $2$、$3$、$3$。
由 ChatGPT 4.1 翻译