CF1986B Matrix Stabilization
题目描述
给你一个大小为 $n \times m$ 的矩阵,矩阵的行从上到下编号为 $1$ 到 $n$,列从左到右编号为 $1$ 到 $m$。矩阵中第 $i$ 行与第 $j$ 列的交点处的元素记为 $a_{ij}$。
我们有一个用于稳定化矩阵 $a$ 的算法:
1. 找到一个单元格 $(i, j)$,该单元格的值严格大于其所有相邻单元格的值。如果没有这样的单元格,则终止算法。如果有多个这样的单元格,选择 $i$ 值最小的单元格;如果仍有多个单元格,选择 $j$ 值最小的单元格。
2. 将 $a_{ij}$ 的值减 1。
3. 回到步骤 1。
在这个问题中,如果两个单元格 $(a, b)$ 和 $(c, d)$ 共享一条边,即 $|a - c| + |b - d| = 1$,则它们被认为是相邻的。
你的任务是输出矩阵 $a$ 在稳定化算法执行后的结果。可以证明,此算法不能无限次运行。
输入格式
每个测试包含多组输入数据。第一行包含一个整数 $t$ ($1 \leq t \leq 10^4$) —— 输入数据的组数。接下来是这些输入数据的描述。
每组输入数据的第一行包含两个整数 $n$ 和 $m$ ($1 \leq n, m \leq 100, n \cdot m > 1$) —— 矩阵 $a$ 的行数和列数。
接下来的 $n$ 行描述了矩阵的相应行。第 $i$ 行包含 $m$ 个整数 $a_{i1}, a_{i2}, \ldots, a_{im}$ ($1 \leq a_{ij} \leq 10^9$)。
保证所有输入数据中 $n \cdot m$ 的总和不超过 $2 \cdot 10^5$。
输出格式
对于每组输入数据,输出 $n$ 行,每行 $m$ 个数,表示矩阵 $a$ 在稳定化算法执行后的值。
## 样例 #1
### 样例输入 #1
说明/提示
In the first set of input data, the algorithm will select the cell $ (1, 1) $ twice in a row and then terminate.
In the second set of input data, there is no cell whose value is strictly greater than the values of all neighboring cells.
In the third set of input data, the algorithm will select the cell $ (2, 2) $ and then terminate.
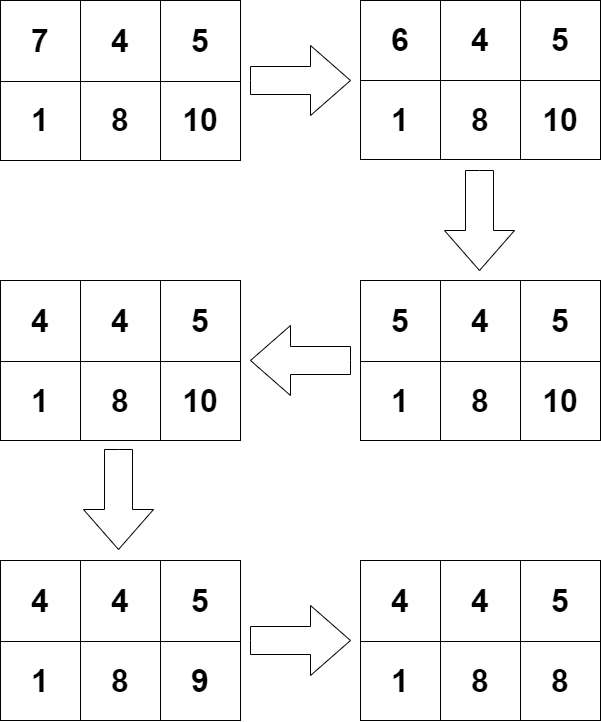
In the fourth set of input data, the algorithm will select the cell $ (1, 1) $ three times and then the cell $ (2, 3) $ twice.