CF1987E Wonderful Tree!

God's Blessing on This ArrayForces! A Random Pebble You are given a tree with $ n $ vertices, rooted at vertex $ 1 $ . The $ i $ -th vertex has an integer $ a_i $ written on it. Let $ L $ be the set of all direct children $ ^{\text{∗}} $ of $ v $ . A tree is called wonderful, if for all vertices $ v $ where $ L $ is not empty, $$ a_v \le \sum_{u \in L}{a_u} $$ In one operation, you choose any vertex $ v $ and increase $ a\_v $ by $ 1 $ . Find the minimum number of operations needed to make the given tree wonderful!. $ ^{\text{∗}} $ Vertex $ u $ is called a direct child of vertex $ v $ if: $ u $ and $ v $ are connected by an edge, and $ v $ is on the (unique) path from $ u $ to the root of the tree.

Each test contains multiple test cases. The first line of input contains a single integer $ t $ ( $ 1 \le t \le 1000 $ ) — the number of test cases. The description of the test cases follows. The first line of each test case contains a single integer $ n $ ( $ 2 \le n \le 5000 $ ) — the number of vertices in the tree. The second line of each test case contains $ n $ integers $ a_1, a_2, \ldots, a_n $ ( $ 0 \le a_i \le 10^9 $ ) — the values initially written on the vertices. The third line of each test case contains $ n - 1 $ integers $ p_2, p_3 , \ldots, p_n $ ( $ 1 \le p_i < i $ ), indicating that there is an edge from vertex $ p_i $ to vertex $ i $ . It is guaranteed that the given edges form a tree. It is guaranteed that the sum of $ n $ over all test cases does not exceed $ 5000 $ .

For each test case, output a single integer — the minimum number of operations needed to make the tree wonderful.

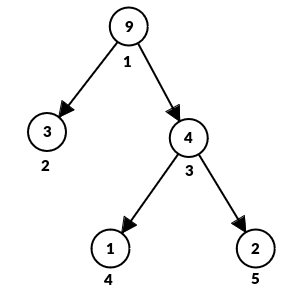The tree in the first test case: You can apply the operation once on vertex $ 5 $ and twice on vertex $ 2 $ to get a wonderful tree. In the second test case, you can apply the operation twice on vertex $ 2 $ to get a wonderful tree. In the third and fourth test cases, the tree is already wonderful, so you don't need to apply any operations.