CF1987G1 Spinning Round (Easy Version)
题目描述
这是该问题的简单版本。两个版本的区别仅在于 $s$ 允许的字符。在简单版本中,$s$ 只包含字符 ?。只有当你同时解决了两个版本的问题时,才能进行 hack。
给定一个长度为 $n$ 的排列 $p$,以及一个长度为 $n$ 只包含字符 ? 的字符串 $s$。
对于每个 $i$,$1 \le i \le n$:
- 定义 $l_i$ 为最大的下标 $j < i$,使得 $p_j > p_i$。如果不存在这样的 $j$,则 $l_i := i$。
- 定义 $r_i$ 为最小的下标 $j > i$,使得 $p_j > p_i$。如果不存在这样的 $j$,则 $r_i := i$。
初始时,你有一个 $n$ 个点(编号为 $1$ 到 $n$)且没有边的无向图。然后,对于每个 $i$,$1 \le i \le n$,向图中添加一条边:
- 如果 $s_i = $ L,则向图中添加边 $(i, l_i)$。
- 如果 $s_i = $ R,则向图中添加边 $(i, r_i)$。
- 如果 $s_i = ?$,你可以选择向图中添加边 $(i, l_i)$ 或 $(i, r_i)$。
请你求出所有你能构造出的连通图中,可能的最大直径 $^{\ast}$。如果无法构造出连通图,输出 $-1$。
$^{\ast}$ 记 $d(s, t)$ 为点 $s$ 和 $t$ 之间任意一条路径上最少的边数。
图的直径定义为所有点对 $(s, t)$ 中 $d(s, t)$ 的最大值。
输入格式
每组测试数据包含多组测试用例。输入的第一行包含一个整数 $t$($1 \le t \le 2 \cdot 10^4$),表示测试用例的组数。接下来是每组测试用例的描述。
每组测试用例的第一行包含一个整数 $n$($2 \le n \le 4 \cdot 10^5$),表示排列 $p$ 的长度。
第二行包含 $n$ 个整数 $p_1, p_2, \ldots, p_n$($1 \le p_i \le n$),表示排列 $p$ 的元素。
第三行包含一个长度为 $n$ 的字符串 $s$,保证只包含字符 ?。
保证所有测试用例中 $n$ 的总和不超过 $4 \cdot 10^5$。
输出格式
对于每组测试用例,输出你能构造出的所有连通图中可能的最大直径。如果无法构造出连通图,输出 $-1$。
说明/提示
在第一个测试用例中,以下是你可以构造的一些连通图(标签为下标):
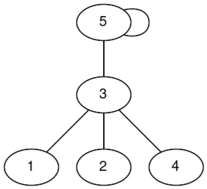
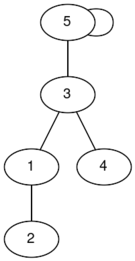
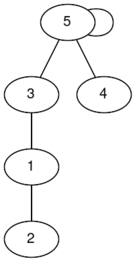
在第二个测试用例中,唯一的连通图的直径为 $1$。
由 ChatGPT 4.1 翻译