CF1987G2 Spinning Round (Hard Version)

This is the hard version of the problem. The only difference between the two versions are the allowed characters in $ s $ . You can make hacks only if both versions of the problem are solved. You are given a permutation $ p $ of length $ n $ . You are also given a string $ s $ of length $ n $ , where each character is either L, R, or ?. For each $ i $ from $ 1 $ to $ n $ : - Define $ l_i $ as the largest index $ j < i $ such that $ p_j > p_i $ . If there is no such index, $ l_i := i $ . - Define $ r_i $ as the smallest index $ j > i $ such that $ p_j > p_i $ . If there is no such index, $ r_i := i $ . Initially, you have an undirected graph with $ n $ vertices (numbered from $ 1 $ to $ n $ ) and no edges. Then, for each $ i $ from $ 1 $ to $ n $ , add one edge to the graph: - If $ s_i = $ L, add the edge $ (i, l_i) $ to the graph. - If $ s_i = $ R, add the edge $ (i, r_i) $ to the graph. - If $ s_i = $ ?, either add the edge $ (i, l_i) $ or the edge $ (i, r_i) $ to the graph at your choice. Find the maximum possible diameter over all connected $ ^{\text{∗}} $ graphs that you can form. Output $ -1 $ if it is not possible to form any connected graphs. $ ^{\text{∗}} $ Let $ d(s, t) $ denote the smallest number of edges on any path between $ s $ and $ t $ . The diameter of the graph is defined as the maximum value of $ d(s, t) $ over all pairs of vertices $ s $ and $ t $ .

Each test contains multiple test cases. The first line of input contains a single integer $ t $ ( $ 1 \le t \le 2 \cdot 10^4 $ ) — the number of test cases. The description of the test cases follows. The first line of each test case contains a single integer $ n $ ( $ 2 \le n \le 4 \cdot 10^5 $ ) — the length of the permutation $ p $ . The second line of each test case contains $ n $ integers $ p_1,p_2,\ldots, p_n $ ( $ 1 \le p_i \le n $ ) — the elements of $ p $ , which are guaranteed to form a permutation. The third line of each test case contains a string $ s $ of length $ n $ . It is guaranteed that it consists only of the characters L, R, and ?. It is guaranteed that the sum of $ n $ over all test cases does not exceed $ 4 \cdot 10^5 $ .

For each test case, output the maximum possible diameter over all connected graphs that you form, or $ -1 $ if it is not possible to form any connected graphs.

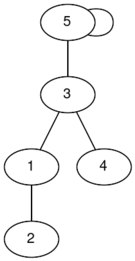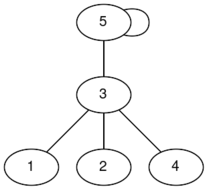In the first test case, there are two connected graphs (the labels are indices): The graph on the left has a diameter of $ 2 $ , while the graph on the right has a diameter of $ 3 $ , so the answer is $ 3 $ . In the second test case, there are no connected graphs, so the answer is $ -1 $ .