CF1990F Polygonal Segments

You are given an array $ a $ of size $ n $ . A segment $ [l, r](1 \le l < r \le n) $ is called a polygonal segment only if the following conditions hold: - $ (r-l+1) \geq 3 $ ; - Considering $ a_l, a_{l+1}, \ldots, a_r $ as side lengths, these sides can form a polygon with $ (r-l+1) $ sides. Process $ q $ queries of two types: - "1 l r": find the length of the longest segment among all polygonal segments $ [l_0,r_0] $ satisfying $ l \le l_0 \le r_0 \le r $ . If there is no such polygonal segment, output $ -1 $ instead; - "2 i x": assign $ a_i := x $ .

The first line contains an integer $ t $ ( $ 1 \leq t \leq 10^4 $ ) — the number of test cases. For each test case: - The first line of each testcase contains two integers $ n $ , $ q $ ( $ 4 \le n \le 2\cdot 10^5 $ , $ 1 \le q \le 10^5 $ ); - The second line of each testcase contains $ n $ integers $ a_1,a_2,\ldots, a_n $ ( $ 1 \le a_i \le 10^{12} $ ); - The following $ q $ lines contain the description of queries. Each line is of one of two types: - "1 l r" ( $ 1 \le l < r \le n $ , $ r-l+1\ge 3 $ ); - "2 i x" ( $ 1 \le i \le n $ , $ 1 \le x \le 10^{12} $ ). It is guaranteed that the sum of $ n $ over all test cases will not exceed $ 2 \cdot 10^5 $ , and the sum of $ q $ over all test cases will not exceed $ 10^5 $ .

For each query, if there is no suitable segment, output $ -1 $ in a new line. Otherwise, output the length of the longest segment satisfying the condition above in a new line.

In the first query of the first test case, there is no polygonal segment under the given condition. For example, considering segment $ [1,3] $ , you can not form a triangle with side lengths of $ a_1=3 $ , $ a_2=1 $ , and $ a_3=2 $ . In the second query of the first test case, the longest polygonal segment is $ [1,4] $ . You can form a quadrilateral with side lengths of $ a_1=3 $ , $ a_2=1 $ , $ a_3=2 $ , and $ a_4=2 $ . 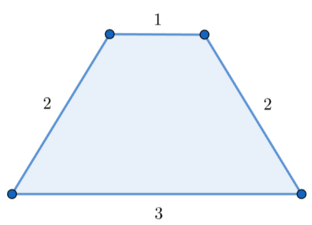 An example of a quadrilateral with side lengths of $ 3 $ , $ 1 $ , $ 2 $ , and $ 2 $ .