CF1990F Polygonal Segments
题目描述
给定一个长度为 $n$ 的数组 $a$。
一个区间 $[l, r]$($1 \le l < r \le n$)被称为多边形区间,当且仅当满足以下条件:
- $r-l+1 \geq 3$;
- 将 $a_l, a_{l+1}, \ldots, a_r$ 作为边长时,这些边可以组成一个有 $r-l+1$ 条边的多边形。
现在有 $q$ 个操作,操作有两种类型:
- “1 l r”:在所有满足 $l \le l_0 \le r_0 \le r$ 的多边形区间 $[l_0, r_0]$ 中,求最长的区间长度。如果不存在这样的多边形区间,输出 $-1$;
- “2 i x”:将 $a_i$ 赋值为 $x$。
输入格式
第一行包含一个整数 $t$($1 \leq t \leq 10^4$),表示测试用例的数量。
对于每个测试用例:
- 每个测试用例的第一行包含两个整数 $n$ 和 $q$($4 \le n \le 2 \cdot 10^5$,$1 \le q \le 10^5$);
- 第二行包含 $n$ 个整数 $a_1,a_2,\ldots, a_n$($1 \le a_i \le 10^{12}$);
- 接下来的 $q$ 行,每行描述一个操作,格式如下:
- “1 l r” ($1 \le l < r \le n$,$r-l+1\ge 3$);
- “2 i x” ($1 \le i \le n$,$1 \le x \le 10^{12}$)。
保证所有测试用例中 $n$ 的总和不超过 $2 \cdot 10^5$,$q$ 的总和不超过 $10^5$。
输出格式
对于每个查询,如果不存在满足条件的区间,输出 $-1$,否则输出满足条件的最长区间的长度,每个结果占一行。
说明/提示
在第一个测试用例的第一个查询中,没有满足条件的多边形区间。例如,考虑区间 $[1,3]$,无法用边长 $a_1=3$、$a_2=1$、$a_3=2$ 组成三角形。
在第一个测试用例的第二个查询中,最长的多边形区间是 $[1,4]$。你可以用边长 $a_1=3$、$a_2=1$、$a_3=2$、$a_4=2$ 组成一个四边形。
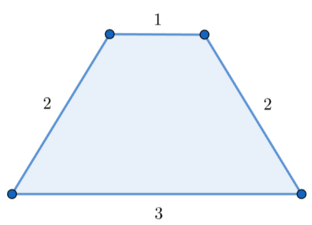 这是一个边长为 $3$、$1$、$2$、$2$ 的四边形示意图。
由 ChatGPT 4.1 翻译