CF1993E Xor-Grid Problem

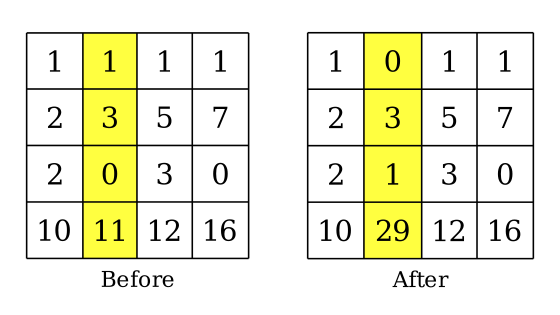
给定一个大小为 $n \times m$ 的矩阵 $a$，每个格子中包含一个非负整数。矩阵第 $i$ 行第 $j$ 列的整数记为 $a_{i,j}$。 我们定义 $f(i)$ 和 $g(j)$ 分别为第 $i$ 行和第 $j$ 列所有整数的 [异或](https://en.wikipedia.org/wiki/Exclusive_or) 值。在一次操作中，你可以： - 选择任意一行 $i$，然后将该行每个元素 $a_{i,j}$（$1 \le j \le m$）赋值为 $g(j)$； - 或选择任意一列 $j$，然后将该列每个元素 $a_{i,j}$（$1 \le i \le n$）赋值为 $f(i)$。  如图所示，对矩阵的第 $2$ 列进行一次操作后，该列所有元素发生了变化： - $a_{1,2} := f(1) = a_{1,1} \oplus a_{1,2} \oplus a_{1,3} \oplus a_{1,4} = 1 \oplus 1 \oplus 1 \oplus 1 = 0$ - $a_{2,2} := f(2) = a_{2,1} \oplus a_{2,2} \oplus a_{2,3} \oplus a_{2,4} = 2 \oplus 3 \oplus 5 \oplus 7 = 3$ - $a_{3,2} := f(3) = a_{3,1} \oplus a_{3,2} \oplus a_{3,3} \oplus a_{3,4} = 2 \oplus 0 \oplus 3 \oplus 0 = 1$ - $a_{4,2} := f(4) = a_{4,1} \oplus a_{4,2} \oplus a_{4,3} \oplus a_{4,4} = 10 \oplus 11 \oplus 12 \oplus 16 = 29$ 你可以进行任意次数的上述操作。最终，我们通过对所有相邻格子的绝对差值求和，得到最终矩阵的 $beauty$。 更正式地，$beauty(a) = \sum|a_{x,y} - a_{r,c}|$，其中 $(x, y)$ 和 $(r, c)$ 是相邻的格子。两个格子相邻当且仅当它们有公共边。 请你求出所有可能得到的矩阵中，$beauty$ 的最小值。

第一行包含一个整数 $t$（$1 \le t \le 250$），表示测试用例的数量。 每个测试用例的第一行包含两个整数 $n$ 和 $m$（$1 \le n, m \le 15$），表示矩阵的行数和列数。 接下来 $n$ 行，每行包含 $m$ 个整数 $a_{i,1}, a_{i,2}, \ldots, a_{i,m}$（$0 \le a_{i,j} < 2^{20}$），表示矩阵 $a$ 的内容。 保证所有测试用例中 $(n^2 + m^2)$ 的总和不超过 $500$。

对于每个测试用例，输出一个整数 $b$，表示所有可能得到的矩阵中 $beauty$ 的最小值。

我们用 $r(i)$ 表示对第 $i$ 行进行第一种操作，用 $c(j)$ 表示对第 $j$ 列进行第二种操作。 在第一个测试用例中，你可以对第 $1$ 列进行一次操作 $c(1)$，将 $a_{1,1} := 1 \oplus 3 = 2$。此时矩阵变为： 23 在第二个测试用例中，你可以对第 $1$ 行进行一次操作 $r(1)$，赋值如下： - $a_{1,1} := g(1) = 0 \oplus 5 = 5$ - $a_{1,2} := g(2) = 1 \oplus 4 = 5$ - $a_{1,3} := g(3) = 0 \oplus 4 = 4$ 操作后矩阵变为： 554 544 在第三个测试用例中，最优方案是依次对第 $3$ 列、第 $2$ 行和第 $2$ 列进行操作，最终矩阵为： 046 456 由 ChatGPT 4.1 翻译