CF1993E Xor-Grid Problem

Given a matrix $ a $ of size $ n \times m $ , each cell of which contains a non-negative integer. The integer lying at the intersection of the $ i $ -th row and the $ j $ -th column of the matrix is called $ a_{i,j} $ . Let's define $ f(i) $ and $ g(j) $ as the [XOR](https://en.wikipedia.org/wiki/Exclusive_or) of all integers in the $ i $ -th row and the $ j $ -th column, respectively. In one operation, you can either: - Select any row $ i $ , then assign $ a_{i,j} := g(j) $ for each $ 1 \le j \le m $ ; or - Select any column $ j $ , then assign $ a_{i,j} := f(i) $ for each $ 1 \le i \le n $ . 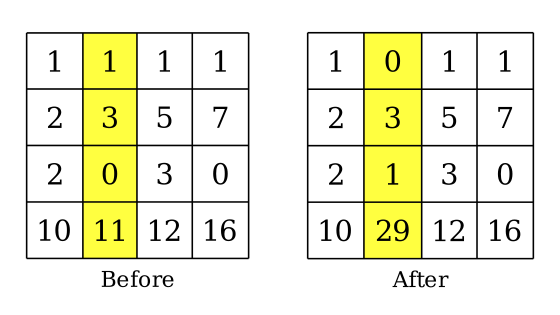 An example of applying an operation on column $ 2 $ of the matrix.In this example, as we apply an operation on column $ 2 $ , all elements in this column are changed: - $ a_{1,2} := f(1) = a_{1,1} \oplus a_{1,2} \oplus a_{1,3} \oplus a_{1,4} = 1 \oplus 1 \oplus 1 \oplus 1 = 0 $ - $ a_{2,2} := f(2) = a_{2,1} \oplus a_{2,2} \oplus a_{2,3} \oplus a_{2,4} = 2 \oplus 3 \oplus 5 \oplus 7 = 3 $ - $ a_{3,2} := f(3) = a_{3,1} \oplus a_{3,2} \oplus a_{3,3} \oplus a_{3,4} = 2 \oplus 0 \oplus 3 \oplus 0 = 1 $ - $ a_{4,2} := f(4) = a_{4,1} \oplus a_{4,2} \oplus a_{4,3} \oplus a_{4,4} = 10 \oplus 11 \oplus 12 \oplus 16 = 29 $ You can apply the operations any number of times. Then, we calculate the $ \textit{beauty} $ of the final matrix by summing the absolute differences between all pairs of its adjacent cells. More formally, $ \textit{beauty}(a) = \sum|a_{x,y} - a_{r,c}| $ for all cells $ (x, y) $ and $ (r, c) $ if they are adjacent. Two cells are considered adjacent if they share a side. Find the minimum $ \textit{beauty} $ among all obtainable matrices.

The first line contains a single integer $ t $ ( $ 1 \le t \le 250 $ ) — the number of test cases. The first line of each test case contains two integers $ n $ and $ m $ ( $ 1 \le n, m \le 15 $ ) — the number of rows and columns of $ a $ , respectively. The next $ n $ lines, each containing $ m $ integers $ a_{i,1}, a_{i,2}, \ldots, a_{i,m} $ ( $ 0 \le a_{i,j} < 2^{20} $ ) — description of the matrix $ a $ . It is guaranteed that the sum of $ (n^2 + m^2) $ over all test cases does not exceed $ 500 $ .

For each test case, print a single integer $ b $ — the smallest possible $ \textit{beauty} $ of the matrix.

Let's denote $ r(i) $ as the first type operation applied on the $ i $ -th row, and $ c(j) $ as the second type operation applied on the $ j $ -th column. In the first test case, you can apply an operation $ c(1) $ , which assigns $ a_{1,1} := 1 \oplus 3 = 2 $ . Then, we'll receive this matrix: 23In the second test case, you can apply an operation $ r(1) $ , which assigns: - $ a_{1,1} := g(1) = 0 \oplus 5 = 5 $ - $ a_{1,2} := g(2) = 1 \oplus 4 = 5 $ - $ a_{1,3} := g(3) = 0 \oplus 4 = 4 $ The resulting matrix after performing the operation is: 554544In the third test case, the best way to achieve minimum $ \textit{beauty} $ is applying three operations: $ c(3) $ , $ r(2) $ , and $ c(2) $ . The resulting matrix is: 046456