CF1993F2 Dyn-scripted Robot (Hard Version)
题目描述
这是该问题的困难版本。唯一的区别在于本版本中 $k \le 10^{12}$。只有当你同时解决了两个版本的问题时,才能进行 hack。
给定一个 $w \times h$ 的矩形,位于 $Oxy$ 平面上,左下角为点 $(0, 0)$,右上角为点 $(w, h)$。
你还有一个初始位于点 $(0, 0)$ 的机器人,以及一个长度为 $n$ 的脚本 $s$。脚本 $s$ 由 $n$ 个字符组成,每个字符为 L、R、U 或 D,分别表示机器人向左、右、上、下移动。
机器人只能在矩形内部移动;如果它试图移出矩形,则会按如下方式更改脚本 $s$:
- 如果它试图越过垂直边界,则将所有 L 字符变为 R(反之亦然,将所有 R 变为 L)。
- 如果它试图越过水平边界,则将所有 U 字符变为 D(反之亦然,将所有 D 变为 U)。
然后,机器人会从无法执行的那个字符开始,执行更改后的脚本。
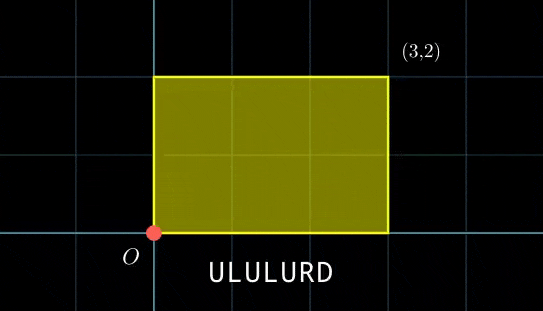
这是机器人的移动过程示例,$s = \texttt{"ULULURD"}$。
脚本 $s$ 会连续执行 $k$ 次。所有对字符串 $s$ 的更改在每次重复时都会保留。在这个过程中,机器人总共会有多少次移动到点 $(0, 0)$?注意,初始位置不计入。
输入格式
第一行包含一个整数 $t$($1 \le t \le 10^4$),表示测试用例的数量。
每个测试用例的第一行包含四个整数 $n$、$k$、$w$ 和 $h$($1 \le n, w, h \le 10^6$;$1 \le k \le 10^{12}$)。
第二行包含一个长度为 $n$ 的字符串 $s$($s_i \in \{\texttt{L}, \texttt{R}, \texttt{U}, \texttt{D}\}$),即要执行的脚本。
保证所有测试用例中 $n$ 的总和不超过 $10^6$。
输出格式
对于每个测试用例,输出一个整数,表示机器人在连续执行 $k$ 次脚本 $s$ 的过程中到达 $(0, 0)$ 的次数。
说明/提示
在第一个测试用例中,机器人前两次只会向上和向右移动。之后,它会停在 $(2, 2)$。接下来的两次执行中,它会向下和向左移动,最终回到 $(0, 0)$。所以答案是 $1$。
在第二个测试用例中,每次执行脚本时,机器人都会访问原点两次。由于 $k=2$,所以总共访问原点 $2 \cdot 2 = 4$ 次。
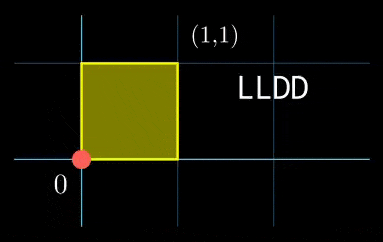
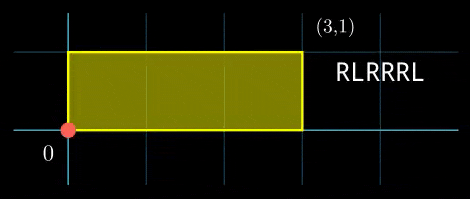
在第三个测试用例中,移动过程可视化如下:
由 ChatGPT 4.1 翻译