CF2002C Black Circles

在一个二维平面上有 $n$ 个圆。第 $i$ 个圆的圆心位于 $(x_i, y_i)$。最初，所有圆的半径都是 $0$。 这些圆的半径以每秒 $1$ 单位的速度增长。 你现在的位置是 $(x_s, y_s)$，你的目标是到达 $(x_t, y_t)$，并且在这个运动过程中不能碰到任何一个圆的边缘（包括你到达 $(x_t, y_t)$ 的那一刻）。你可以向任意方向移动。然而，你的速度被限制在每秒 $1$ 单位。 请判断是否有可能实现这一目标。

每个测试样例包含多个测试用例。第一行包含测试用例的数量 $t$（$1 \le t \le 10^4$）。接着是各个测试用例的描述。 每个测试用例的第一行包含一个整数 $n$（$1 \le n \le 10^5$）——圆的数量。 接下来的 $n$ 行，每行包含两个整数 $x_i$ 和 $y_i$（$1 \le x_i, y_i \le 10^9$）——每个圆的圆心坐标。 最后一行包含四个整数 $x_s$，$y_s$，$x_t$，$y_t$（$1 \le x_s, y_s, x_t, y_t \le 10^9$）——起点和终点的坐标。 题目保证这 $n+2$ 个点是互不相同的。 题目还保证所有测试用例中 $n$ 的总和不超过 $10^5$。

对于每一个测试用例，如果能够不接触任何圆的边缘就能到达目标，则输出 $\texttt{YES}$，否则输出 $\texttt{NO}$。 你可以不区分大小写输出 $\texttt{YES}$ 和 $\texttt{NO}$（例如，$\texttt{yEs}$、$\texttt{yes}$、$\texttt{Yes}$ 和 $\texttt{YES}$ 都会被认为是肯定的回答）。

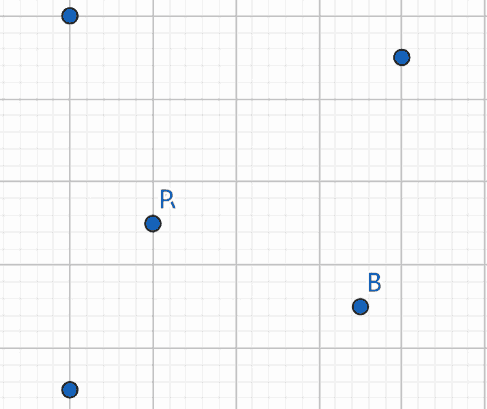
在第一个测试用例中，一种可行的移动方式如下图所示。