CF2002G Lattice Optimizing

考虑一个具有 $n$ 行和 $n$ 列的网格图。 对于所有 $x < n$ 的位置有一个权值 $d_{x,y}$ 对于所有 $y < n$ 的位置有一个权值 $r_{x,y}$ 从 $(1,1)$ 开始走，每次往下或往右走，最终到 $(n,n)$。 初始有一个空集合 $S$。若从 $(x,y)$ 走到 $(x+1,y)$，将 $d_{x,y}$ 加入 $S$；走到 $(x,y+1)$ 就加入 $r_{x,y}$。 需要最大化走到终点时的 $mex(S)$ 其中，$mex(x)$ 定义为 $x$ 中最小未出现的 **非负整数**。

第一行一个数 $T$，表示测试组数。 每组测试第一行一个整数 $n$，接下来 $n-1$ 行每行 $n$ 个数表示 $d$。 接下来 $n$ 行每行 $n-1$ 个数表示 $r$。 保证 $n$ 不超过 $20$，且所有 $n^3$ 的和不超过 $8000$，且 $d_{i,j}$ 和 $r_{i,j}$ 都不超过 $2n-2$。

输出 $T$ 行表示每组测试数据的答案。

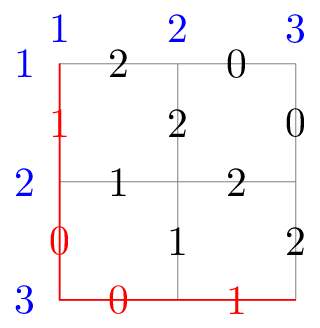
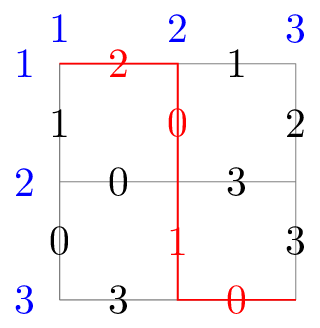In the first test case, the grid graph and one of the optimal paths are as follows: In the second test case, the grid graph and one of the optimal paths are as follows: