CF2002G Lattice Optimizing

Consider a grid graph with $ n $ rows and $ n $ columns. Let the cell in row $ x $ and column $ y $ be $ (x,y) $ . There exists a directed edge from $ (x,y) $ to $ (x+1,y) $ , with non-negative integer value $ d_{x,y} $ , for all $ 1\le x < n, 1\le y \le n $ , and there also exists a directed edge from $ (x,y) $ to $ (x,y+1) $ , with non-negative integer value $ r_{x,y} $ , for all $ 1\le x \le n, 1\le y < n $ . Initially, you are at $ (1,1) $ , with an empty set $ S $ . You need to walk along the edges and eventually reach $ (n,n) $ . Whenever you pass an edge, its value will be inserted into $ S $ . Please maximize the MEX $ ^{\text{∗}} $ of $ S $ when you reach $ (n,n) $ . $ ^{\text{∗}} $ The MEX (minimum excluded) of an array is the smallest non-negative integer that does not belong to the array. For instance: - The MEX of $ [2,2,1] $ is $ 0 $ , because $ 0 $ does not belong to the array. - The MEX of $ [3,1,0,1] $ is $ 2 $ , because $ 0 $ and $ 1 $ belong to the array, but $ 2 $ does not. - The MEX of $ [0,3,1,2] $ is $ 4 $ , because $ 0, 1, 2 $ , and $ 3 $ belong to the array, but $ 4 $ does not.

Each test contains multiple test cases. The first line contains the number of test cases $ t $ ( $ 1\le t\le100 $ ). The description of the test cases follows. The first line of each test case contains a single integer $ n $ ( $ 2\le n\le20 $ ) — the number of rows and columns. Each of the next $ n-1 $ lines contains $ n $ integers separated by single spaces — the matrix $ d $ ( $ 0\le d_{x,y}\le 2n-2 $ ). Each of the next $ n $ lines contains $ n-1 $ integers separated by single spaces — the matrix $ r $ ( $ 0\le r_{x,y}\le 2n-2 $ ). It is guaranteed that the sum of all $ n^3 $ does not exceed $ 8000 $ .

For each test case, print a single integer — the maximum MEX of $ S $ when you reach $ (n,n) $ .

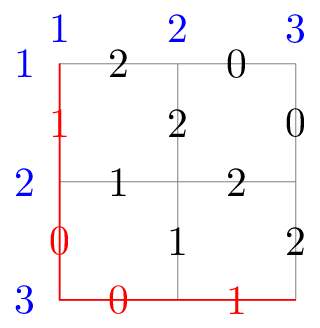
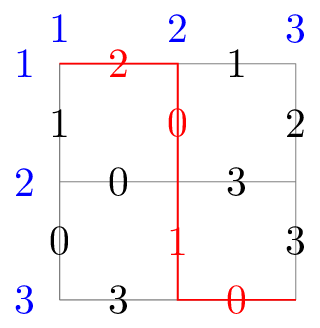In the first test case, the grid graph and one of the optimal paths are as follows: In the second test case, the grid graph and one of the optimal paths are as follows: