CF2006A Iris and Game on the Tree

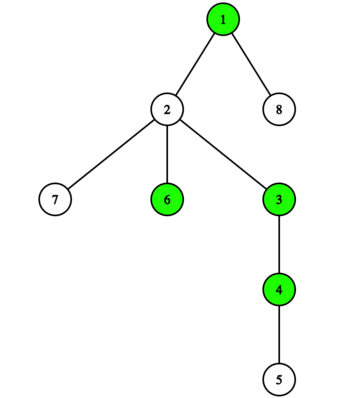
给定一棵根为 $1$，每个点有 $0$ 或 $1$ 的点权的有根树，对于所有叶子定义权值为：取出根到它的路径上所有点的点权形成的 $01$ 串，其中 $10$ 子串的出现次数减去 $01$ 子串的出现次数。不认为根为叶子。  如图，绿点的点权为 $1$，白点的点权为 $0$，根到 $5$ 的串为 $10110$，其中有 $2$ 个 $10$，$1$ 个 $01$，故 $5$ 的权值为 $1$。 一棵树的分数被定义为：具有非零权值的叶子的数量。 有些点权尚未确定，A 与 B 在玩游戏，她们轮流将一个未确定点的点权改为 $0$ 或 $1$。先手的 A 希望最大化树的分数，后手的 B 希望最小化之，二人均采取最优策略，求最后树的分数。

第一行输入一个数 $t$ 表示数据范围。 对于每组数据，第一行输入一个数 $n$ 表示树的点数，后面 $n-1$ 行每行两个数字代表树的一条边。最后一行有一个长度为 $n$ 的字符串 $s$，仅包含 `?`，`0` 和 `1`，若第 $i$ 位为 `?` 则说明点 $i$ 的权值尚未确定，否则说明点 $i$ 的权值为 $s_i$。

对于每组数据，输出一行一个数，表示最后树的分数。

$1 \leq t \leq 5 \cdot 10^4$，$2 \leq \sum n \leq 2 \cdot 10^5$。 translated by uid 443664