CF2006B Iris and the Tree
题目描述
给定一棵以 $1$ 号结点为根的有根树。对于树中任意结点 $i$($1 < i \leq n$),存在一条连接结点 $i$ 和 $p_i$($1 \leq p_i < i$)的边,边权为 $t_i$。
Iris 并不知道所有 $t_i$ 的具体值,但她知道 $\displaystyle\sum_{i=2}^n t_i = w$,且每个 $t_i$ 都是非负整数。
树的结点编号有特殊要求:每个子树中的结点编号是连续的整数。换句话说,树的结点编号是按照深度优先遍历的顺序排列的。
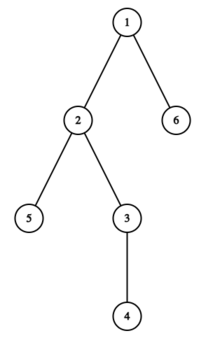
上图中的树满足条件。例如,结点 $2$ 的子树中,结点编号为 $2, 3, 4, 5$,是连续的整数。
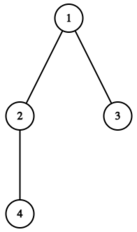
上图中的树不满足条件,因为结点 $2$ 的子树中,结点编号 $2$ 和 $4$ 不是连续的整数。
我们定义 $\operatorname{dist}(u, v)$ 为树中结点 $u$ 和 $v$ 之间的简单路径长度。
接下来有 $n-1$ 个事件:
- Iris 得到两个整数 $x$ 和 $y$,表示 $t_x = y$。
每次事件后,Iris 想要分别独立地计算每个 $i$($1 \leq i \leq n$)时 $\operatorname{dist}(i, i \bmod n + 1)$ 的最大可能值。她只需要知道这 $n$ 个值的和。请你帮助 Iris 快速得到答案。
注意,在分别计算 $\operatorname{dist}(i, i \bmod n + 1)$ 和 $\operatorname{dist}(j, j \bmod n + 1)$($i \ne j$)的最大可能值时,未知的边权可以不同。
输入格式
每个测试点包含多组测试数据。第一行包含一个整数 $t$($1 \leq t \leq 10^4$),表示测试数据组数。每组测试数据描述如下:
每组测试数据的第一行包含两个整数 $n$ 和 $w$($2 \leq n \leq 2 \cdot 10^5$,$0 \leq w \leq 10^{12}$),表示树的结点数和边权和。
第二行包含 $n-1$ 个整数 $p_2, p_3, \ldots, p_n$($1 \leq p_i < i$),表示树的边的描述。
接下来有 $n-1$ 行,每行两个整数 $x$ 和 $y$($2 \leq x \leq n$,$0 \leq y \leq w$),表示 $t_x = y$。
保证所有事件中的 $x$ 互不相同,且所有 $y$ 的和等于 $w$。
保证所有测试数据中 $n$ 的总和不超过 $2 \cdot 10^5$。
输出格式
对于每组测试数据,输出一行包含 $n-1$ 个整数,分别表示每次事件后的答案。
说明/提示
在第一个测试点中,$\operatorname{dist}(1, 2) = \operatorname{dist}(2, 1) = t_2 = w = 10^{12}$,所以 $\operatorname{dist}(1, 2) + \operatorname{dist}(2, 1) = 2 \cdot 10^{12}$。
在第二个测试点中,Iris 得知所有 $t_x$ 后的树如下图:
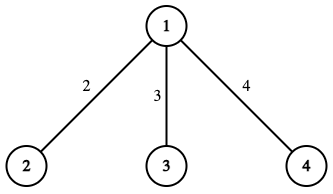
$\operatorname{dist}(1, 2) = t_2$,$\operatorname{dist}(2, 3) = t_2 + t_3$,$\operatorname{dist}(3, 4) = t_3 + t_4$,$\operatorname{dist}(4, 1) = t_4$。第一次事件后,$t_2 = 2$,所以 $\operatorname{dist}(1, 2) = 2$。同时:
- 若 $t_3 = 7$,$t_4 = 0$,则 $\operatorname{dist}(2, 3)$ 最大为 $9$。
- 若 $t_3 = 0$,$t_4 = 7$,则 $\operatorname{dist}(3, 4)$ 和 $\operatorname{dist}(4, 1)$ 最大为 $7$。
因此,答案为 $2 + 9 + 7 + 7 = 25$。
第二次事件后,$t_4 = 4$,则 $t_3 = w - t_2 - t_4 = 4$。$\operatorname{dist}(1, 2) = 2$,$\operatorname{dist}(2, 3) = 2 + 3 = 5$,$\operatorname{dist}(3, 4) = 3 + 4 = 7$,$\operatorname{dist}(4, 1) = 4$。因此,答案为 $2 + 5 + 7 + 4 = 18$。
由 ChatGPT 4.1 翻译