CF2006B Iris and the Tree

Given a rooted tree with the root at vertex $ 1 $ . For any vertex $ i $ ( $ 1 < i \leq n $ ) in the tree, there is an edge connecting vertices $ i $ and $ p_i $ ( $ 1 \leq p_i < i $ ), with a weight equal to $ t_i $ . Iris does not know the values of $ t_i $ , but she knows that $ \displaystyle\sum_{i=2}^n t_i = w $ and each of the $ t_i $ is a non-negative integer. The vertices of the tree are numbered in a special way: the numbers of the vertices in each subtree are consecutive integers. In other words, the vertices of the tree are numbered in the order of a depth-first search. 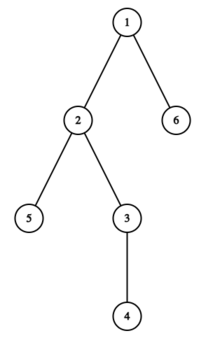 The tree in this picture satisfies the condition. For example, in the subtree of vertex $ 2 $ , the vertex numbers are $ 2, 3, 4, 5 $ , which are consecutive integers. 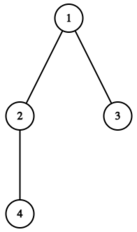 The tree in this picture does not satisfy the condition, as in the subtree of vertex $ 2 $ , the vertex numbers $ 2 $ and $ 4 $ are not consecutive integers.We define $ \operatorname{dist}(u, v) $ as the length of the simple path between vertices $ u $ and $ v $ in the tree. Next, there will be $ n - 1 $ events: - Iris is given integers $ x $ and $ y $ , indicating that $ t_x = y $ . After each event, Iris wants to know the maximum possible value of $ \operatorname{dist}(i, i \bmod n + 1) $ independently for each $ i $ ( $ 1\le i\le n $ ). She only needs to know the sum of these $ n $ values. Please help Iris quickly get the answers. Note that when calculating the maximum possible values of $ \operatorname{dist}(i, i \bmod n + 1) $ and $ \operatorname{dist}(j, j \bmod n + 1) $ for $ i \ne j $ , the unknown edge weights may be different.

Each test consists of multiple test cases. The first line contains a single integer $ t $ ( $ 1 \leq t \leq 10^4 $ ) — the number of test cases. The description of the test cases follows. The first line of each test case contains two integers $ n $ and $ w $ ( $ 2 \le n \le 2 \cdot 10^5 $ , $ 0 \leq w \leq 10^{12} $ ) — the number of vertices in the tree and the sum of the edge weights. The second line of each test case contains $ n - 1 $ integers $ p_2, p_3, \ldots, p_n $ ( $ 1 \leq p_i < i $ ) — the description of the edges of the tree. Then follow $ n-1 $ lines indicating the events. Each line contains two integers $ x $ and $ y $ ( $ 2 \leq x \leq n $ , $ 0 \leq y \leq w $ ), indicating that $ t_x = y $ . It is guaranteed that all $ x $ in the events are distinct. It is also guaranteed that the sum of all $ y $ equals $ w $ . It is guaranteed that the sum of $ n $ over all test cases does not exceed $ 2 \cdot 10^5 $ .

For each test case, output one line containing $ n-1 $ integers, each representing the answer after each event.

In the first test case, $ \operatorname{dist}(1, 2) = \operatorname{dist}(2, 1) = t_2 = w = 10^{12} $ , so $ \operatorname{dist}(1, 2) + \operatorname{dist}(2, 1) = 2 \cdot 10^{12} $ . In the second test case, the tree after Iris found out all $ t_x $ is shown below: 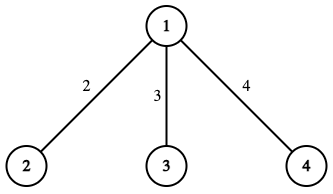 $ \operatorname{dist}(1, 2) = t_2 $ , $ \operatorname{dist}(2, 3) = t_2 + t_3 $ , $ \operatorname{dist}(3, 4) = t_3 + t_4 $ , $ \operatorname{dist}(4, 1) = t_4 $ . After the first event, she found out that $ t_2 = 2 $ , so $ \operatorname{dist}(1, 2) = 2 $ . At the same time: - $ \operatorname{dist}(2, 3) $ is maximized if $ t_3 = 7 $ , $ t_4 = 0 $ . Then $ \operatorname{dist}(2, 3) = 9 $ . - $ \operatorname{dist}(3, 4) $ and $ \operatorname{dist}(4, 1) $ are maximized if $ t_3 = 0 $ , $ t_4 = 7 $ . Then $ \operatorname{dist}(3, 4) = \operatorname{dist}(4, 1) = 7 $ . Thus, the answer is $ 2 + 9 + 7 + 7 = 25 $ . After the second event, she found out that $ t_4 = 4 $ , then $ t_3 = w - t_2 - t_4 = 4 $ . $ \operatorname{dist}(1, 2) = 2 $ , $ \operatorname{dist}(2, 3) = 2 + 3 = 5 $ , $ \operatorname{dist}(3, 4) = 3 + 4 = 7 $ , $ \operatorname{dist}(4, 1) = 4 $ . Thus, the answer is $ 2 + 5 + 7 + 4 = 18 $ .