CF2006E Iris's Full Binary Tree

Iris likes full binary trees. Let's define the depth of a rooted tree as the maximum number of vertices on the simple paths from some vertex to the root. A full binary tree of depth $ d $ is a binary tree of depth $ d $ with exactly $ 2^d - 1 $ vertices. Iris calls a tree a $ d $ -binary tree if some vertices and edges can be added to it to make it a full binary tree of depth $ d $ . Note that any vertex can be chosen as the root of a full binary tree. Since performing operations on large trees is difficult, she defines the binary depth of a tree as the minimum $ d $ satisfying that the tree is $ d $ -binary. Specifically, if there is no integer $ d \ge 1 $ such that the tree is $ d $ -binary, the binary depth of the tree is $ -1 $ . Iris now has a tree consisting of only vertex $ 1 $ . She wants to add $ n - 1 $ more vertices to form a larger tree. She will add the vertices one by one. When she adds vertex $ i $ ( $ 2 \leq i \leq n $ ), she'll give you an integer $ p_i $ ( $ 1 \leq p_i < i $ ), and add a new edge connecting vertices $ i $ and $ p_i $ . Iris wants to ask you the binary depth of the tree formed by the first $ i $ vertices for each $ 1 \le i \le n $ . Can you tell her the answer?

Each test consists of multiple test cases. The first line contains a single integer $ t $ ( $ 1 \leq t \leq 10^4 $ ) — the number of test cases. The description of the test cases follows. The first line of each test case contains a single integer $ n $ ( $ 2 \leq n \leq 5 \cdot 10^5 $ ) — the final size of the tree. The second line of each test case contains $ n - 1 $ integers $ p_2, p_3, \ldots, p_n $ ( $ 1 \leq p_i < i $ ) — descriptions of all edges of the tree. It is guaranteed that the sum of $ n $ over all test cases does not exceed $ 5 \cdot 10^5 $ .

For each test case output $ n $ integers, $ i $ -th of them representing the binary depth of the tree formed by the first $ i $ vertices.

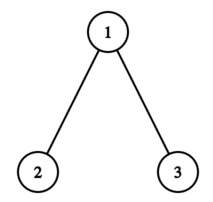In the first test case, the final tree is shown below: - The tree consisting of the vertex $ 1 $ has the binary depth $ 1 $ (the tree itself is a full binary tree of depth $ 1 $ ). - The tree consisting of the vertices $ 1 $ and $ 2 $ has the binary depth $ 2 $ (we can add the vertex $ 3 $ to make it a full binary tree of depth $ 2 $ ). - The tree consisting of the vertices $ 1 $ , $ 2 $ and $ 3 $ has the binary depth $ 2 $ (the tree itself is a full binary tree of depth $ 2 $ ). 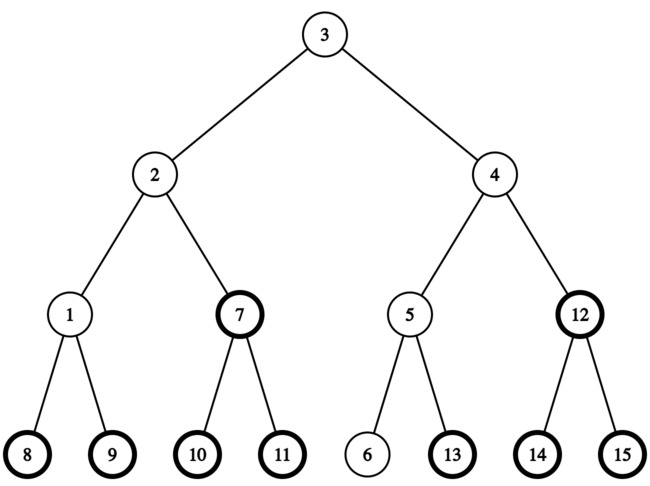In the second test case, the formed full binary tree after adding some vertices to the tree consisting of $ n $ vertices is shown below (bolded vertices are added): The depth of the formed full binary tree is $ 4 $ . 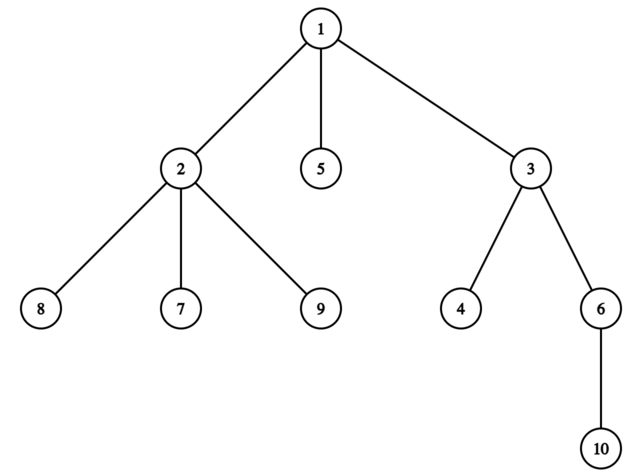In the fifth test case, the final tree is shown below: It can be proved that Iris can't form any full binary tree by adding vertices and edges, so the binary depth is $ -1 $ .