CF2006E Iris's Full Binary Tree

Iris 喜欢满二叉树。 我们定义一棵有根树的深度为从某个顶点到根的简单路径上顶点的最大数量。深度为 $d$ 的满二叉树是一棵深度为 $d$ 且恰好有 $2^d - 1$ 个顶点的二叉树。 Iris 称一棵树为 $d$-二叉树，如果可以通过添加一些顶点和边，使其变为一棵深度为 $d$ 的满二叉树。注意，满二叉树的根可以任选任意顶点。 由于在大树上操作很困难，她定义了一棵树的二叉深度为满足该树是 $d$-二叉树的最小 $d$。具体地说，如果不存在整数 $d \ge 1$ 使得该树是 $d$-二叉树，则该树的二叉深度为 $-1$。 现在，Iris 有一棵仅包含顶点 $1$ 的树。她想再添加 $n-1$ 个顶点，形成一棵更大的树。她会依次添加这些顶点。当她添加第 $i$ 个顶点（$2 \leq i \leq n$）时，会给你一个整数 $p_i$（$1 \leq p_i < i$），并添加一条连接顶点 $i$ 和 $p_i$ 的新边。 Iris 想请你告诉她，对于每个 $1 \le i \le n$，由前 $i$ 个顶点组成的树的二叉深度是多少。你能告诉她答案吗？

每个测试用例包含多组数据。第一行包含一个整数 $t$（$1 \leq t \leq 10^4$）——表示测试用例的数量。接下来是每组测试用例的描述。 每组测试用例的第一行包含一个整数 $n$（$2 \leq n \leq 5 \cdot 10^5$）——表示树的最终大小。 第二行包含 $n-1$ 个整数 $p_2, p_3, \ldots, p_n$（$1 \leq p_i < i$）——描述树的所有边。 保证所有测试用例中 $n$ 的总和不超过 $5 \cdot 10^5$。

对于每组测试用例，输出 $n$ 个整数，第 $i$ 个表示由前 $i$ 个顶点组成的树的二叉深度。

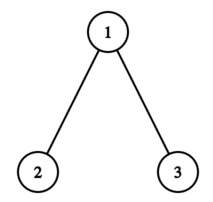
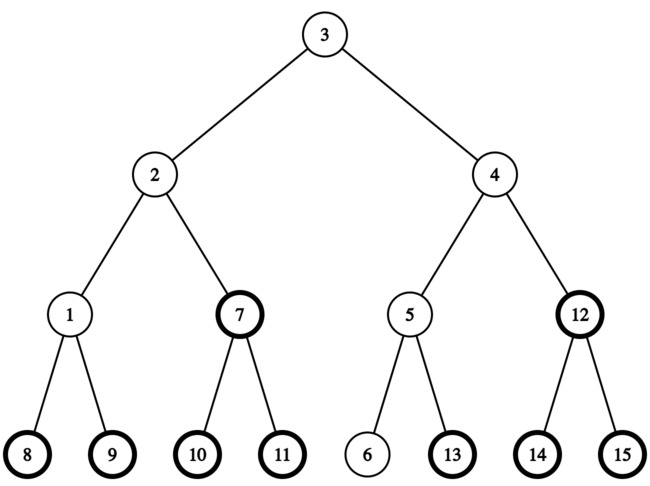
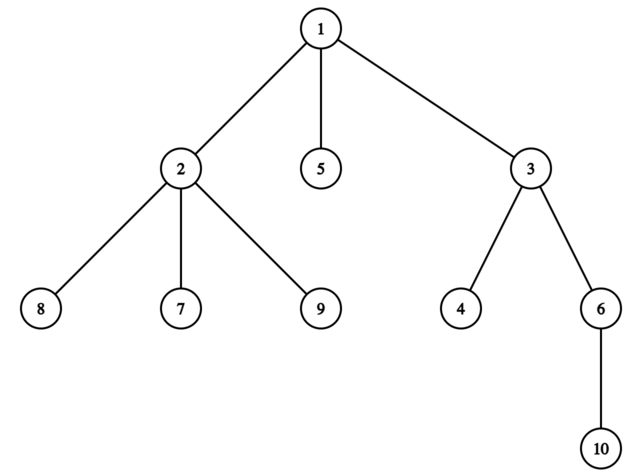
在第一个测试用例中，最终的树如下图所示：  - 仅包含顶点 $1$ 的树的二叉深度为 $1$（该树本身就是深度为 $1$ 的满二叉树）。 - 包含顶点 $1$ 和 $2$ 的树的二叉深度为 $2$（我们可以添加顶点 $3$ 使其成为深度为 $2$ 的满二叉树）。 - 包含顶点 $1$、$2$ 和 $3$ 的树的二叉深度为 $2$（该树本身就是深度为 $2$ 的满二叉树）。 在第二个测试用例中，添加一些顶点后形成的满二叉树如下图所示（加粗的顶点为新添加的）：  形成的满二叉树的深度为 $4$。 在第五个测试用例中，最终的树如下图所示：  可以证明，Iris 无法通过添加顶点和边形成任何满二叉树，因此二叉深度为 $-1$。 由 ChatGPT 4.1 翻译