CF2008B Square or Not

A beautiful binary matrix is a matrix that has ones on its edges and zeros inside. 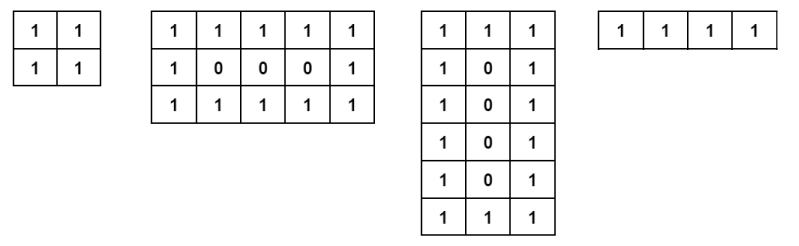 Examples of four beautiful binary matrices.Today, Sakurako was playing with a beautiful binary matrix of size $ r \times c $ and created a binary string $ s $ by writing down all the rows of the matrix, starting from the first and ending with the $ r $ -th. More formally, the element from the matrix in the $ i $ -th row and $ j $ -th column corresponds to the $ ((i-1)*c+j) $ -th element of the string. You need to check whether the beautiful matrix from which the string $ s $ was obtained could be squared. In other words, you need to check whether the string $ s $ could have been build from a square beautiful binary matrix (i.e., one where $ r=c $ ).

The first line contains a single integer $ t $ ( $ 1 \le t \le 10^4 $ ) — the number of test cases. The first line of each test case contains a single integer $ n $ ( $ 2 \le n \le 2 \cdot 10^5 $ ) — the length of the string. The second line of each test case contains the string $ s $ of length $ n $ . The string is always the result of writing out the strings of a beautiful matrix. It is guaranteed that the sum of $ n $ across all test cases does not exceed $ 2 \cdot 10^5 $ .

Print "Yes", if the original matrix could have been square, and "No" otherwise.

For the second test case, string 1111 can be obtained from the matrix: $ 1 $ $ 1 $ $ 1 $ $ 1 $ For the third test case, string 111101111 can be obtained from the matrix: $ 1 $ $ 1 $ $ 1 $ $ 1 $ $ 0 $ $ 1 $ $ 1 $ $ 1 $ $ 1 $ There is no square matrix in the fourth case, such that the string can be obtained from it.