CF2013F2 Game in Tree (Hard Version)

This is the hard version of the problem. In this version, it is not guaranteed that $ u = v $ . You can make hacks only if both versions of the problem are solved. Alice and Bob are playing a fun game on a tree. This game is played on a tree with $ n $ vertices, numbered from $ 1 $ to $ n $ . Recall that a tree with $ n $ vertices is an undirected connected graph with $ n - 1 $ edges. Alice and Bob take turns, with Alice going first. Each player starts at some vertex. On their turn, a player must move from the current vertex to a neighboring vertex that has not yet been visited by anyone. The first player who cannot make a move loses. You are given two vertices $ u $ and $ v $ . Represent the simple path from vertex $ u $ to $ v $ as an array $ p_1, p_2, p_3, \ldots, p_m $ , where $ p_1 = u $ , $ p_m = v $ , and there is an edge between $ p_i $ and $ p_{i + 1} $ for all $ i $ ( $ 1 \le i < m $ ). You need to determine the winner of the game if Alice starts at vertex $ 1 $ and Bob starts at vertex $ p_j $ for each $ j $ (where $ 1 \le j \le m $ ).

Each test contains multiple test cases. The first line contains the number of test cases $ t $ ( $ 1 \le t \le 10^4 $ ). The description of the test cases follows. The first line of each test case contains a single integer $ n $ ( $ 2 \le n \le 2 \cdot 10^5 $ ) — the number of vertices in the tree. Each of the following $ n - 1 $ lines contains two integers $ a $ and $ b $ ( $ 1 \le a, b \le n $ ), denoting an undirected edge between vertices $ a $ and $ b $ . It is guaranteed that these edges form a tree. The last line of each test case contains two integers $ u $ and $ v $ ( $ 2 \le u, v \le n $ ). It is guaranteed that the path from $ u $ to $ v $ does not pass through vertex $ 1 $ . It is guaranteed that the sum of $ n $ over all test cases does not exceed $ 2 \cdot 10^5 $ .

For each test case, output $ m $ lines. In the $ i $ -th line, print the winner of the game if Alice starts at vertex $ 1 $ and Bob starts at vertex $ p_i $ . Print "Alice" (without quotes) if Alice wins, or "Bob" (without quotes) otherwise.

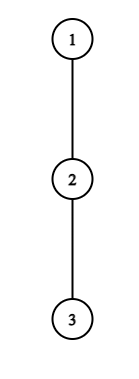 Tree from the first example.In the first test case, the path will be ( $ 2,3 $ ). If Bob starts at vertex $ 2 $ , Alice will not be able to move anywhere on her first turn and will lose. However, if Bob starts at vertex $ 3 $ , Alice will move to vertex $ 2 $ , and Bob will have no remaining vertices to visit and will lose.