CF2018C Tree Pruning

[t+pazolite, ginkiha, Hommarju - Paved Garden](https://soundcloud.com/fractalex-gd/ginkiha-paved-garden-little) ⠀ You are given a tree with $ n $ nodes, rooted at node $ 1 $ . In this problem, a leaf is a non-root node with degree $ 1 $ . In one operation, you can remove a leaf and the edge adjacent to it (possibly, new leaves appear). What is the minimum number of operations that you have to perform to get a tree, also rooted at node $ 1 $ , where all the leaves are at the same distance from the root?

Each test contains multiple test cases. The first line contains the number of test cases $ t $ ( $ 1 \le t \le 10^4 $ ). The description of the test cases follows. The first line of each test case contains a single integer $ n $ ( $ 3 \leq n \leq 5 \cdot 10^5 $ ) — the number of nodes. Each of the next $ n-1 $ lines contains two integers $ u $ , $ v $ ( $ 1 \leq u, v \leq n $ , $ u \neq v $ ), describing an edge that connects $ u $ and $ v $ . It is guaranteed that the given edges form a tree. It is guaranteed that the sum of $ n $ over all test cases does not exceed $ 5 \cdot 10^5 $ .

For each test case, output a single integer: the minimum number of operations needed to achieve your goal.

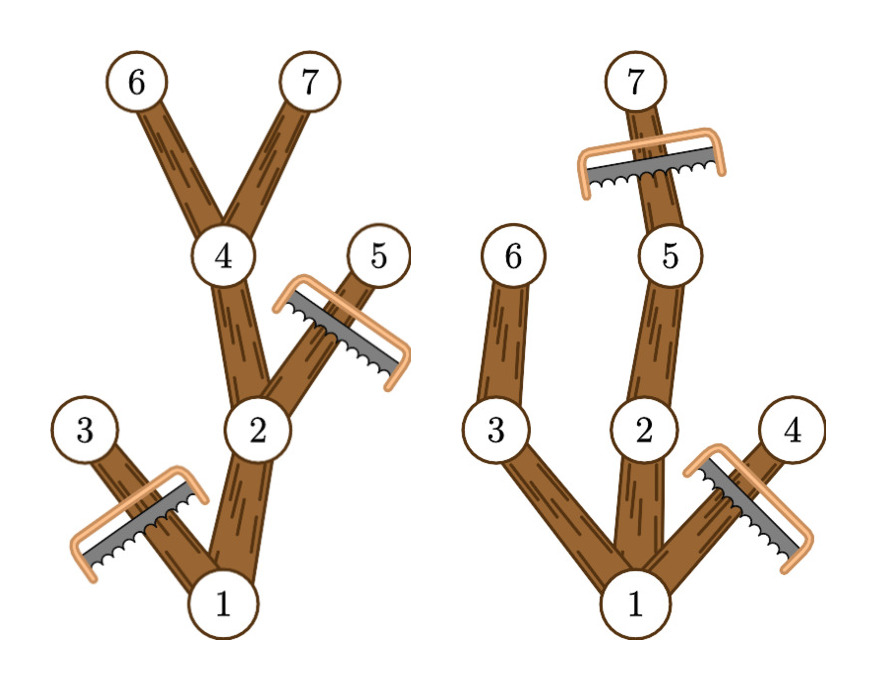In the first two examples, the tree is as follows: In the first example, by removing edges $ (1, 3) $ and $ (2, 5) $ , the resulting tree has all leaves (nodes $ 6 $ and $ 7 $ ) at the same distance from the root (node $ 1 $ ), which is $ 3 $ . The answer is $ 2 $ , as it is the minimum number of edges that need to be removed to achieve the goal. In the second example, removing edges $ (1, 4) $ and $ (5, 7) $ results in a tree where all leaves (nodes $ 4 $ and $ 5 $ ) are at the same distance from the root (node $ 1 $ ), which is $ 2 $ .