CF201A Clear Symmetry
题目描述
给定一个边长为 $n$ 的方阵 $A$,其中元素仅由 $0$ 和 $1$ 组成。矩阵共有 $n$ 行,从上到下编号为 $1$ 到 $n$,$n$ 列,从左到右编号为 $1$ 到 $n$。我们用 $A_{i,j}$ 表示第 $i$ 行第 $j$ 列的元素。
我们称矩阵 $A$ 是“清晰的”,当且仅当矩阵中任意两格包含 $1$ 的单元格没有公共边。
我们称矩阵 $A$ 是“对称的”,当且仅当它在水平和/或垂直翻转后与原矩阵完全一致。形式化地,对每个 $1 \leq i,j \leq n$,都要满足:$A_{i,j} = A_{n-i+1,j}$ 且 $A_{i,j} = A_{i,n-j+1}$。
我们定义矩阵 $A$ 的“锐度”为其中 $1$ 的数量。
给定整数 $x$,请你找出最小的正整数 $n$,使得存在一个边长为 $n$ 的清晰对称矩阵 $A$,其锐度为 $x$。
输入格式
输入仅包含一个整数 $x$($1 \leq x \leq 100$),表示矩阵的目标锐度。
输出格式
输出一个整数,表示所需的最小 $n$。
说明/提示
下图展示了与样例对应的矩阵:
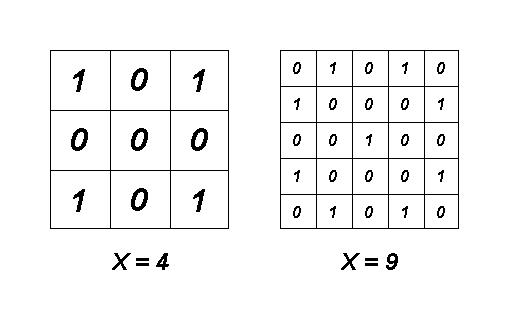
由 ChatGPT 5 翻译