CF201A Clear Symmetry

Consider some square matrix $ A $ with side $ n $ consisting of zeros and ones. There are $ n $ rows numbered from $ 1 $ to $ n $ from top to bottom and $ n $ columns numbered from $ 1 $ to $ n $ from left to right in this matrix. We'll denote the element of the matrix which is located at the intersection of the $ i $ -row and the $ j $ -th column as $ A_{i,j} $ . Let's call matrix $ A $ clear if no two cells containing ones have a common side. Let's call matrix $ A $ symmetrical if it matches the matrices formed from it by a horizontal and/or a vertical reflection. Formally, for each pair $ (i,j) $ $ (1

The only line contains a single integer $ x $ ( $ 1

Print a single number — the sought value of $ n $ .

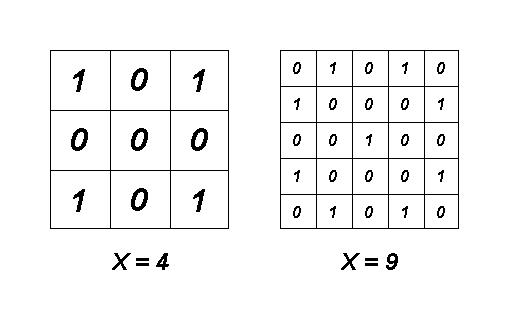
The figure below shows the matrices that correspond to the samples: