CF2020F Count Leaves
题目描述
有正整数 $n$ 和 $d$。我们按如下规则建一棵 $T_{n,d}$ 的约数树:
- 树的根节点上的数为 $n$。这是树的第 $0$ 层。
- 对于第 $i$ 层($i=0,1,...,d-1$)的每个结点,执行如下操作:若当前节点上的数为 $x$,则 $x$ 的所有可能的不同约数为其儿子节点上的数。这些儿子节点位于第 $i+1$ 层。
- 第 $d$ 层上的点为叶子节点。
例如,$T_{6,2}$($n=6,d=2$ 的约数树)如下图所示:
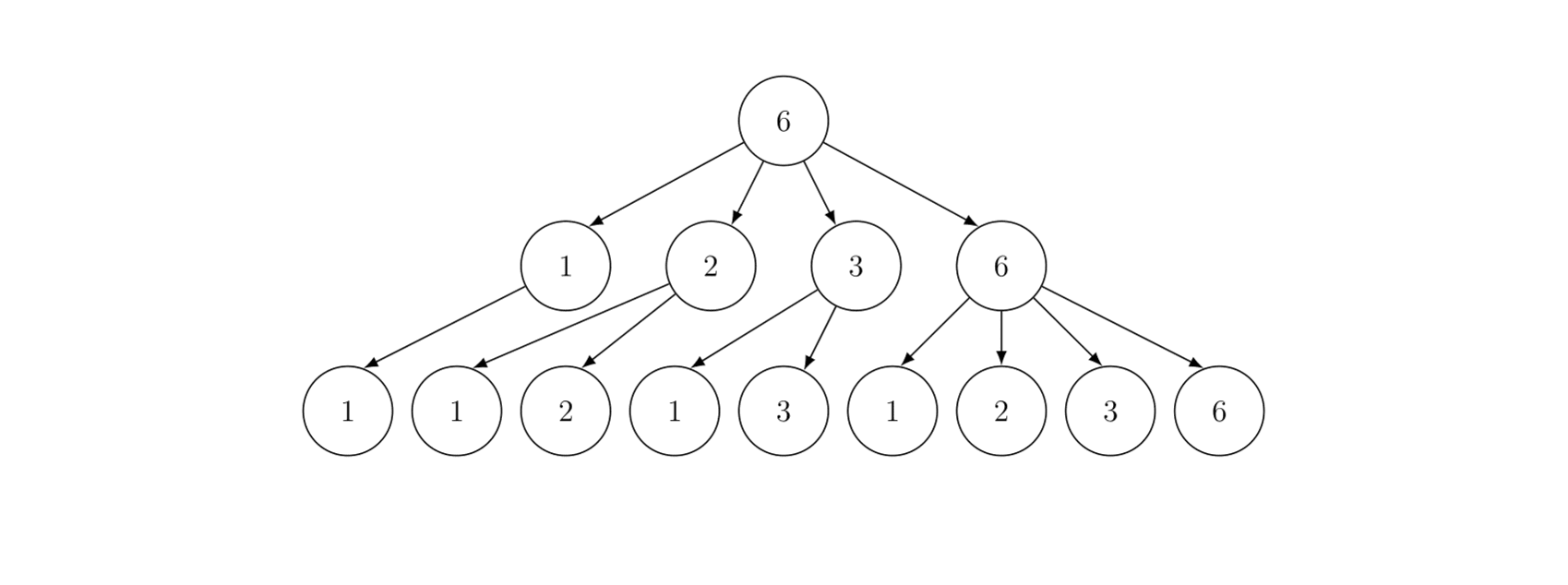
定义 $f(n,d)$ 为 $T(n,d)$ 的叶子节点数。
给定 $n,k,d$ ,计算 $\sum\limits_{i=1}^nf(i^k,d)$ 模 $10^9+7$ 后的答案。
注:在这个问题中,我们说 $y$ 为 $x$ 的约数当且仅当 $y\geq1$ 且存在整数 $z$ 使得 $x=y\cdot z$。
输入格式
每个测试有多组测试数据。第一行 $t\ (1\leq t\leq10^4)$ 为测试数据数。
每个测试数据包含一行三个数 $n,k,d\ (1\leq n\leq 10^9,1\leq k,d\leq 10^5)$。
保证所有测试数据中 $n$ 的和不超过 $10^9$。
输出格式
对于每个测试数据,输出一行一个整数,表示 $\sum\limits_{i=1}^nf(i^k,d)\ mod\ 10^9+7$ 后的结果。
### 样例解释
在第一个测试样例中,$n=6,k=1,d=1$。因此,我们要算出 $T_{1,1},T_{2,1},T_{3,1},T_{4,1},T_{5,1},T_{6,1}$ 的叶子数的和。
- $T_{1,1}$ 只有一个叶子,该叶子上的数为 $1$。
- $T_{2,1}$ 有两个叶子,叶子上的数为 $1,2$。
- $T_{3,1}$ 有两个叶子,叶子上的数为 $1,3$。
- $T_{4,1}$ 有三个叶子,叶子上的数为 $1,2,4$。
- $T_{5,1}$ 有两个叶子,叶子上的数为 $1,5$。
- $T_{6,1}$ 有四个叶子,叶子上的数为 $1,2,3,6$。
叶子的总数为 $1+2+2+3+2+4=14$。
在第二个测试样例中,$n=1,k=3,d=3$,所以我们要求出 $T_{1^3,3}$ 的叶子数。因为 $1^3=1$,所以这棵树只有一片叶子,答案为 $1$。
说明/提示
In the first test case, $ n = 6 $ , $ k = 1 $ , and $ d = 1 $ . Thus, we need to find the total number of leaves in the divisor trees $ T_{1,1} $ , $ T_{2,1} $ , $ T_{3,1} $ , $ T_{4,1} $ , $ T_{5,1} $ , $ T_{6,1} $ .
- $ T_{1,1} $ has only one leaf, which is marked with $ 1 $ .
- $ T_{2,1} $ has two leaves, marked with $ 1 $ and $ 2 $ .
- $ T_{3,1} $ has two leaves, marked with $ 1 $ and $ 3 $ .
- $ T_{4,1} $ has three leaves, marked with $ 1 $ , $ 2 $ , and $ 4 $ .
- $ T_{5,1} $ has two leaves, marked with $ 1 $ and $ 5 $ .
- $ T_{6,1} $ has four leaves, marked with $ 1 $ , $ 2 $ , $ 3 $ , and $ 6 $ .
The total number of leaves is $ 1 + 2 + 2 + 3 + 2 + 4 = 14 $ .
In the second test case, $ n = 1 $ , $ k = 3 $ , $ d = 3 $ . Thus, we need to find the number of leaves in $ T_{1,3} $ , because $ 1^3 = 1 $ . This tree has only one leaf, so the answer is $ 1 $ .