CF2020F Count Leaves

Let $ n $ and $ d $ be positive integers. We build the the divisor tree $ T_{n,d} $ as follows: - The root of the tree is a node marked with number $ n $ . This is the $ 0 $ -th layer of the tree. - For each $ i $ from $ 0 $ to $ d - 1 $ , for each vertex of the $ i $ -th layer, do the following. If the current vertex is marked with $ x $ , create its children and mark them with all possible distinct divisors $ ^\dagger $ of $ x $ . These children will be in the $ (i+1) $ -st layer. - The vertices on the $ d $ -th layer are the leaves of the tree. 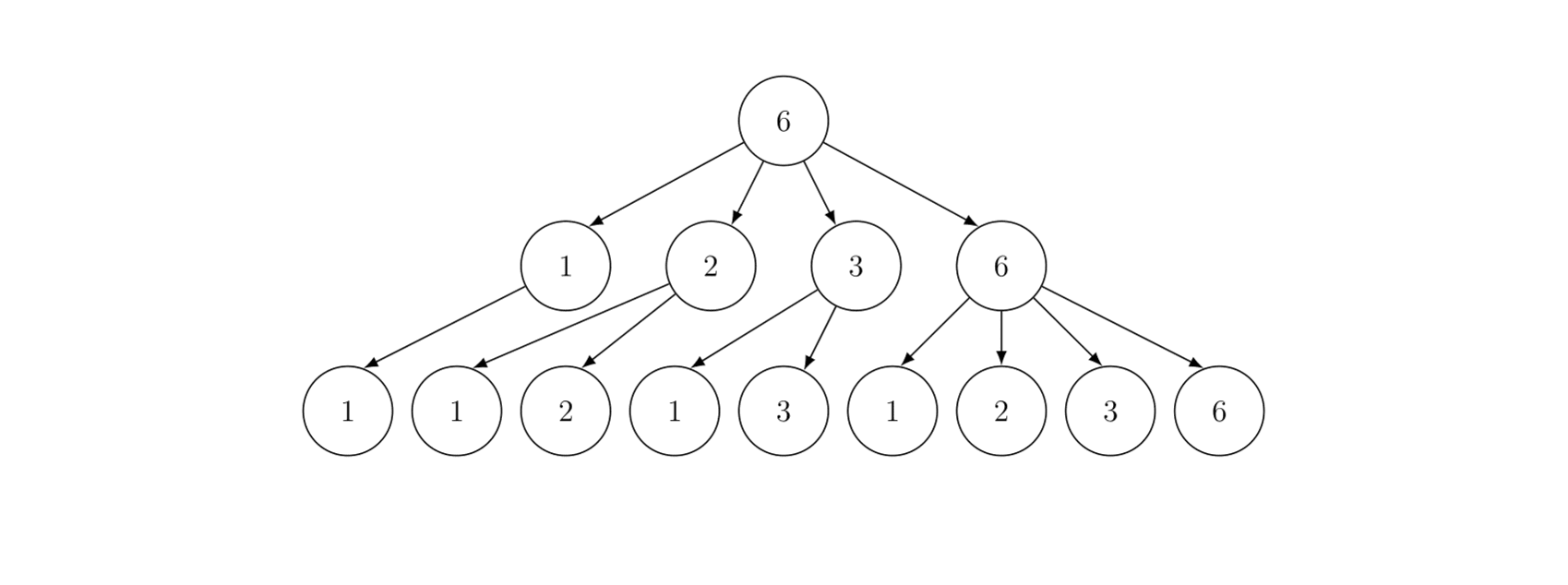For example, $ T_{6,2} $ (the divisor tree for $ n = 6 $ and $ d = 2 $ ) looks like this: Define $ f(n,d) $ as the number of leaves in $ T_{n,d} $ . Given integers $ n $ , $ k $ , and $ d $ , please compute $ \sum\limits_{i=1}^{n} f(i^k,d) $ , modulo $ 10^9+7 $ . $ ^\dagger $ In this problem, we say that an integer $ y $ is a divisor of $ x $ if $ y \ge 1 $ and there exists an integer $ z $ such that $ x = y \cdot z $ .

Each test contains multiple test cases. The first line contains the number of test cases $ t $ ( $ 1 \le t \le 10^4 $ ). The description of the test cases follows. The only line of each test case contains three integers $ n $ , $ k $ , and $ d $ ( $ 1 \le n \le 10^9 $ , $ 1 \le k,d \le 10^5 $ ). It is guaranteed that the sum of $ n $ over all test cases does not exceed $ 10^9 $ .

For each test case, output $ \sum\limits_{i=1}^{n} f(i^k,d) $ , modulo $ 10^9+7 $ .

In the first test case, $ n = 6 $ , $ k = 1 $ , and $ d = 1 $ . Thus, we need to find the total number of leaves in the divisor trees $ T_{1,1} $ , $ T_{2,1} $ , $ T_{3,1} $ , $ T_{4,1} $ , $ T_{5,1} $ , $ T_{6,1} $ . - $ T_{1,1} $ has only one leaf, which is marked with $ 1 $ . - $ T_{2,1} $ has two leaves, marked with $ 1 $ and $ 2 $ . - $ T_{3,1} $ has two leaves, marked with $ 1 $ and $ 3 $ . - $ T_{4,1} $ has three leaves, marked with $ 1 $ , $ 2 $ , and $ 4 $ . - $ T_{5,1} $ has two leaves, marked with $ 1 $ and $ 5 $ . - $ T_{6,1} $ has four leaves, marked with $ 1 $ , $ 2 $ , $ 3 $ , and $ 6 $ . The total number of leaves is $ 1 + 2 + 2 + 3 + 2 + 4 = 14 $ . In the second test case, $ n = 1 $ , $ k = 3 $ , $ d = 3 $ . Thus, we need to find the number of leaves in $ T_{1,3} $ , because $ 1^3 = 1 $ . This tree has only one leaf, so the answer is $ 1 $ .