CF2021D Boss, Thirsty

Pak Chanek的一个朋友在食堂经营一个饮料摊位。他的朋友将在 $n$ 天内出售饮料，从第1天到第 $n$ 天。总共有 $m$ 种饮料，编号从1到 $m$。 在某一天出售某种饮料所能获得的利润会有所不同。在第 $i$ 天，出售第 $j$ 种饮料的预期利润是 $A_{i, j}$。请注意，$A_{i, j}$ 可能是负数，这意味着出售这种饮料实际上会造成亏损。 Pak Chanek想帮助他的朋友规划这 $n$ 天的销售。在第 $i$ 天，Pak Chanek必须选择至少出售一种类型的饮料。此外，在同一天出售的饮料类型必须形成一个子数组。换句话说，在每一天，Pak Chanek将选择 $i$ 和 $j$，满足 $1 \leq i \leq j \leq m$。然后，从第 $i$ 个到第 $j$ 个（包括两端）的所有类型的饮料都将被出售。 但是，为了确保前一天的顾客能继续光顾，第 $i$ 天（$i>1$）出售的饮料类型选择必须满足以下条件： - 第 $i$ 天至少有一种饮料类型也必须在第$i-1$ 天出售。 - 第 $i$ 天至少有一种饮料类型不能在第 $i-1$ 天出售。 每日利润是当天出售的所有饮料类型利润的总和。销售计划的总利润是 $n$ 天内利润的总和。如果Pak Chanek能够优化销售计划，那么他能获得的最大总利润是多少？

每个测试包含多个测试用例。第一行包含测试用例的数量 $t$（$1 \le t \le 1000$）。以下是测试用例的描述。 每个测试用例的第一行包含两个整数 $n$ 和 $m$（$1 \leq n \leq 2 \cdot 10^5$；$3 \leq m \leq 2 \cdot 10^5$；$n \cdot m \leq 2 \cdot 10^5$），表示网格的行数和列数。 每个测试用例的接下来 $n$ 行每行包含 $m$ 个整数，其中第$i$行包含整数 $A_{i,1} A_{i,2}, \ldots, A_{i,m}$（$-10^9 \leq A_{i,j} \leq 10^9$），表示第$i$天每种饮料类型的预期利润。 保证所有测试用例中 $n \cdot m$ 的总和不超过 $2 \cdot 10^5$。

对于每个测试用例，输出一个整数：Pak Chanek能够获得的最大利润。

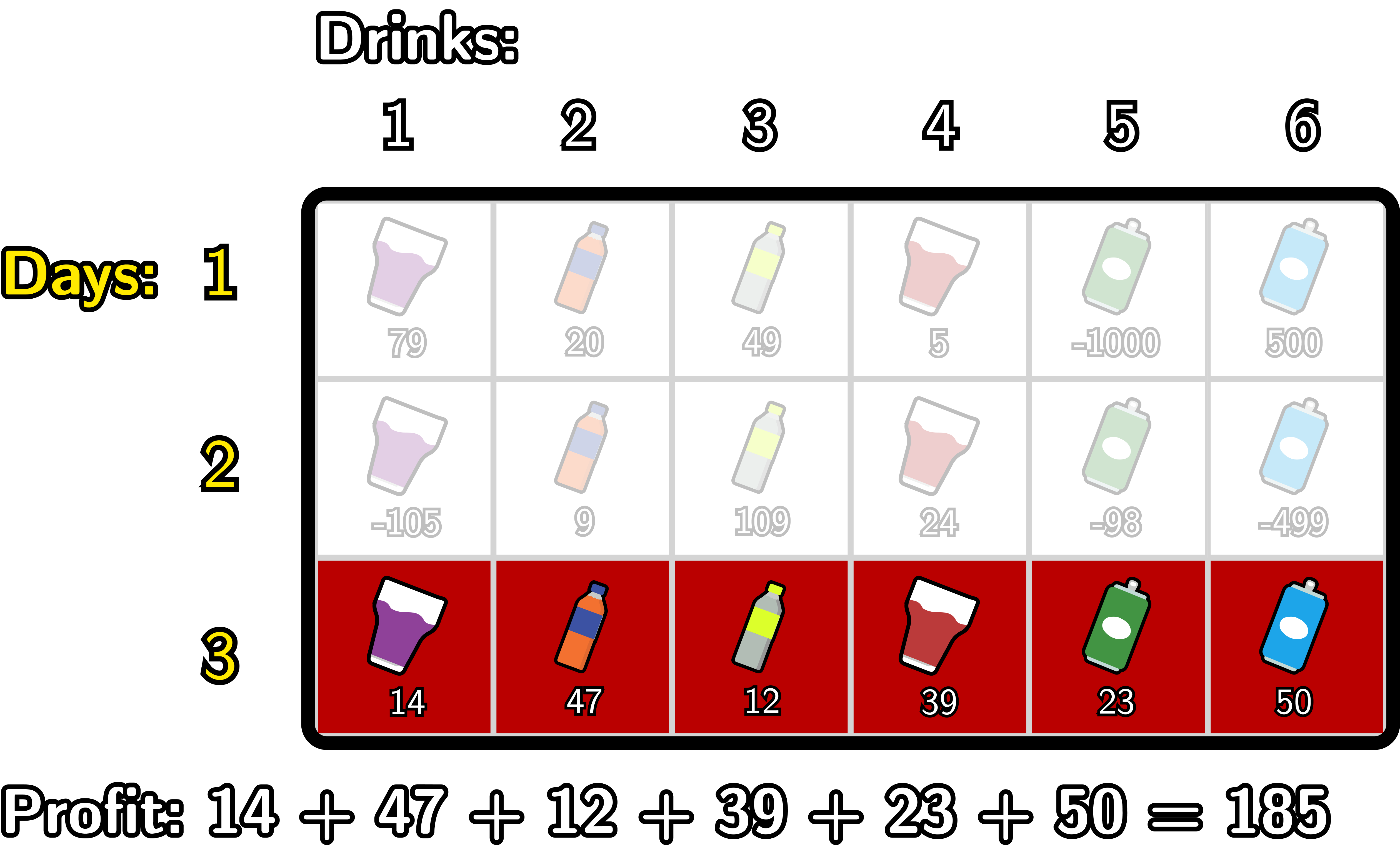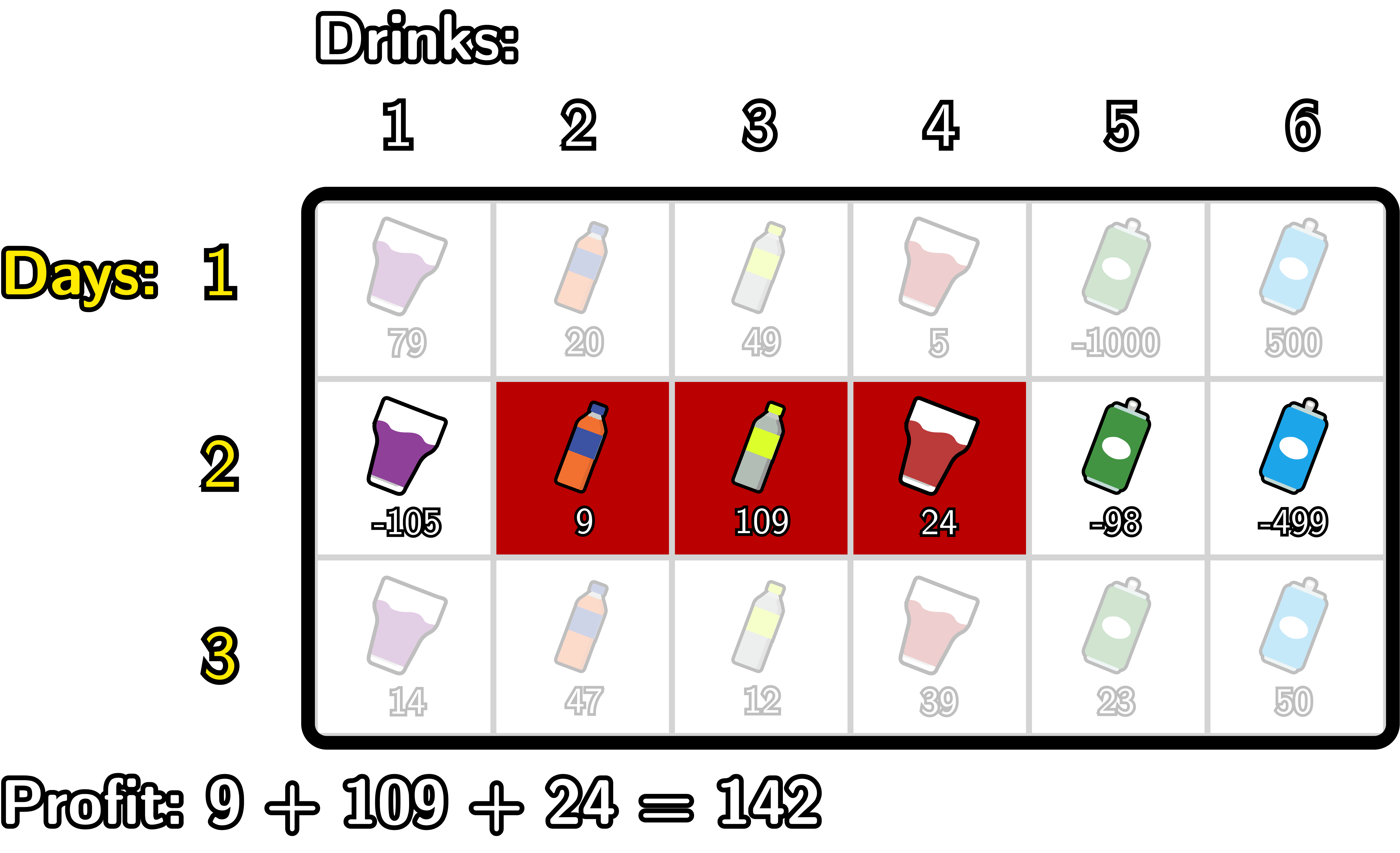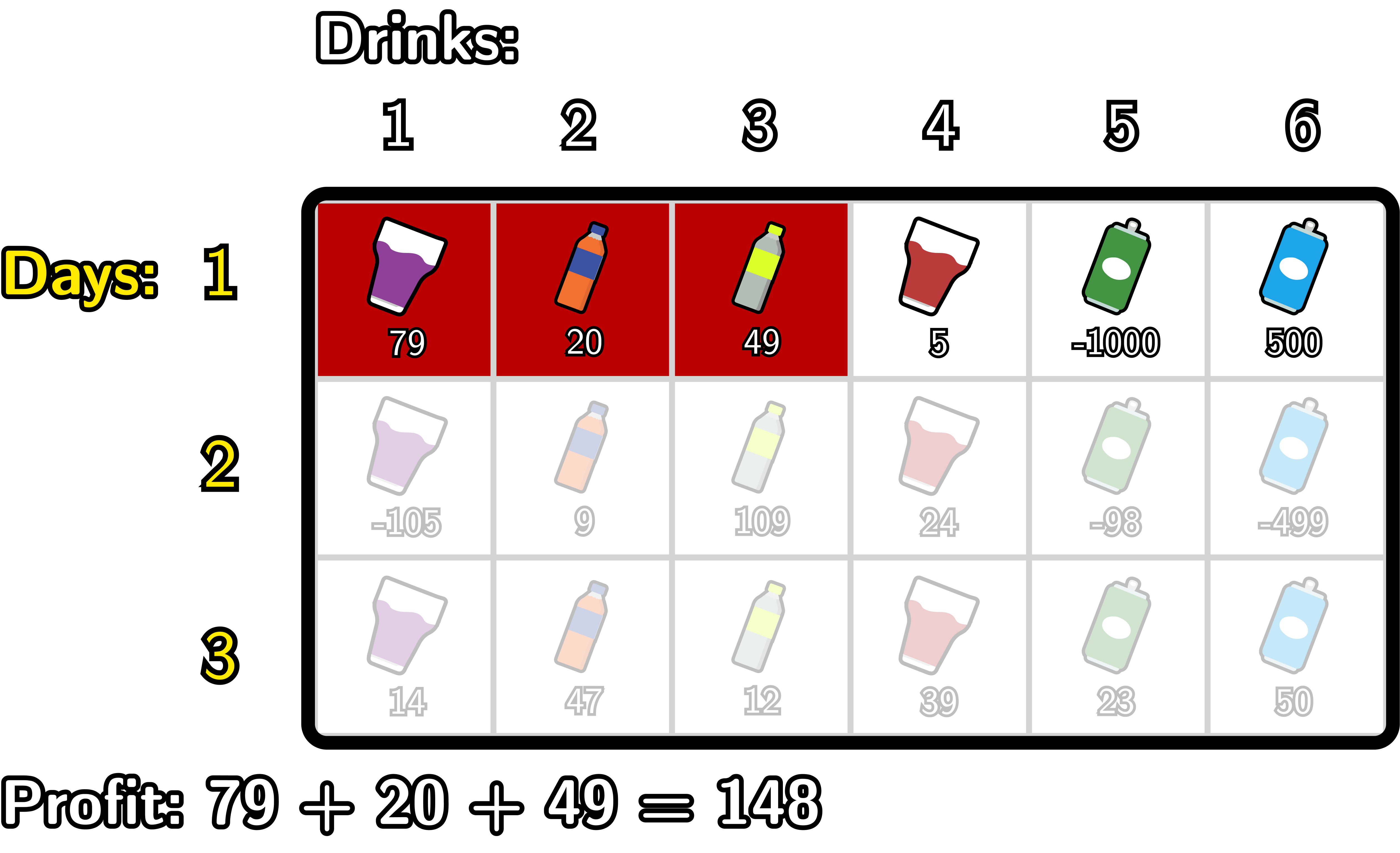
 以下是Pak Chanek的最优计划： - 在第1天，Pak Chanek出售第1到3种饮料。获得利润 $79+20+49 = 148$。 - 在第2天，Pak Chanek出售第2到4种饮料。获得利润 $9+109+24 = 142$。 - 在第3天，Pak Chanek出售第1到6种饮料。获得利润 $185$。 因此，Pak Chanek计划的总利润是 $148 + 142 + 185 = 475$。