CF2022C Gerrymandering

我们都会偷一点点。但我只有一只手，而我的对手有两只。 Álvaro Obregón Álvaro 和 José 是唯一竞选 Tepito 总统的候选人。Tepito 是一个 $2$ 行 $n$ 列的矩形网格，每个格子代表一座房子。保证 $n$ 是 $3$ 的倍数。 在 Tepito 的投票制度下，网格会被划分为若干个选区，每个选区由任意 $3$ 个连通的房子组成 $^{\text{∗}}$。每个房子恰好属于一个选区。 每个选区会投出一票。如果该选区中至少有 $2$ 个房子选择某位候选人，则该选区会投给这位候选人。因此，总共会投出 $\frac{2n}{3}$ 票。 作为现任总统，Álvaro 知道每个房子会选择哪位候选人。如果 ÁLvaro 最优地划分选区，请你求出他最多能获得多少票。 $^{\text{∗}}$ 一组格子是连通的，当且仅当任意两个格子之间存在一条路径，只经过该组格子，并且每一步只能上下左右移动。

每组测试数据包含多个测试用例。第一行包含一个整数 $t$（$1 \le t \le 10^4$），表示测试用例的数量。接下来是每个测试用例的描述。 每个测试用例的第一行包含一个整数 $n$（$3 \le n \le 10^5$，$n$ 是 $3$ 的倍数），表示 Tepito 的列数。 接下来的两行，每行包含一个长度为 $n$ 的字符串。第 $i$ 行的字符串 $s_i$ 由字符 $\texttt{A}$ 和 $\texttt{J}$ 组成。如果 $s_{i,j} = \texttt{A}$，则第 $i$ 行第 $j$ 列的房子会选择 Álvaro；如果 $s_{i,j} = \texttt{J}$，则会选择 José。 保证所有测试用例中 $n$ 的总和不超过 $10^5$。

对于每个测试用例，输出一个整数，表示 Álvaro 最优划分选区后最多能赢得的选区数量。

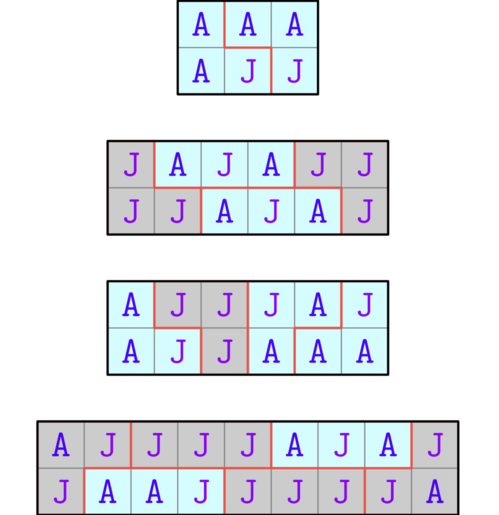
下图展示了样例中每个测试用例的最优选区划分方式。  由 ChatGPT 4.1 翻译