CF2026A Perpendicular Segments

You are given a coordinate plane and three integers $ X $ , $ Y $ , and $ K $ . Find two line segments $ AB $ and $ CD $ such that 1. the coordinates of points $ A $ , $ B $ , $ C $ , and $ D $ are integers; 2. $ 0 \le A_x, B_x, C_x, D_x \le X $ and $ 0 \le A_y, B_y, C_y, D_y \le Y $ ; 3. the length of segment $ AB $ is at least $ K $ ; 4. the length of segment $ CD $ is at least $ K $ ; 5. segments $ AB $ and $ CD $ are perpendicular: if you draw lines that contain $ AB $ and $ CD $ , they will cross at a right angle. Note that it's not necessary for segments to intersect. Segments are perpendicular as long as the lines they induce are perpendicular.

The first line contains a single integer $ t $ ( $ 1 \le t \le 5000 $ ) — the number of test cases. Next, $ t $ cases follow. The first and only line of each test case contains three integers $ X $ , $ Y $ , and $ K $ ( $ 1 \le X, Y \le 1000 $ ; $ 1 \le K \le 1414 $ ). Additional constraint on the input: the values of $ X $ , $ Y $ , and $ K $ are chosen in such a way that the answer exists.

For each test case, print two lines. The first line should contain $ 4 $ integers $ A_x $ , $ A_y $ , $ B_x $ , and $ B_y $ — the coordinates of the first segment. The second line should also contain $ 4 $ integers $ C_x $ , $ C_y $ , $ D_x $ , and $ D_y $ — the coordinates of the second segment. If there are multiple answers, print any of them.

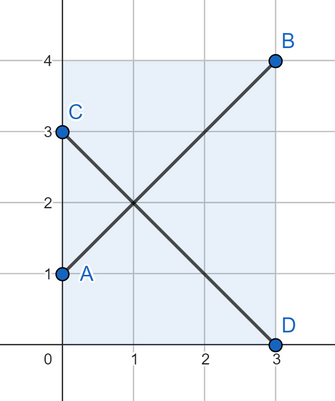
The answer for the first test case is shown below: 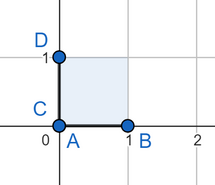 The answer for the second test case: 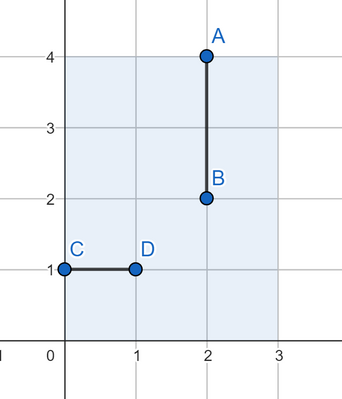 The answer for the third test case: 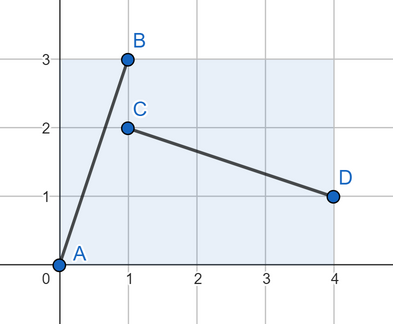 The answer for the fourth test case: