CF2027A Rectangle Arrangement

你正在给一个无限大的方格网格上色，初始时所有格子都是白色的。为此，你有 $n$ 个印章。每个印章是一个宽为 $w_i$、高为 $h_i$ 的矩形。 你将每个印章恰好使用一次，在网格上以黑色涂色一个与印章大小相同的矩形。你不能旋转印章，并且对于每个格子，印章要么完全覆盖它，要么完全不覆盖它。你可以将印章放在网格上的任意位置，即使被盖住的区域部分或全部已经是黑色也没关系。 在所有印章都使用完后，你能得到的黑色方格连通区域的周长之和的最小值是多少？

每个测试点包含多组测试数据。第一行包含测试用例数 $t$（$1 \le t \le 500$）。接下来是每组测试数据的描述。 每组测试数据的第一行包含一个整数 $n$（$1 \le n \le 100$）。 接下来的 $n$ 行中，第 $i$ 行包含两个整数 $w_i$ 和 $h_i$（$1 \le w_i, h_i \le 100$）。

对于每组测试数据，输出一个整数，表示在所有印章都使用后，黑色连通区域的周长之和的最小值。

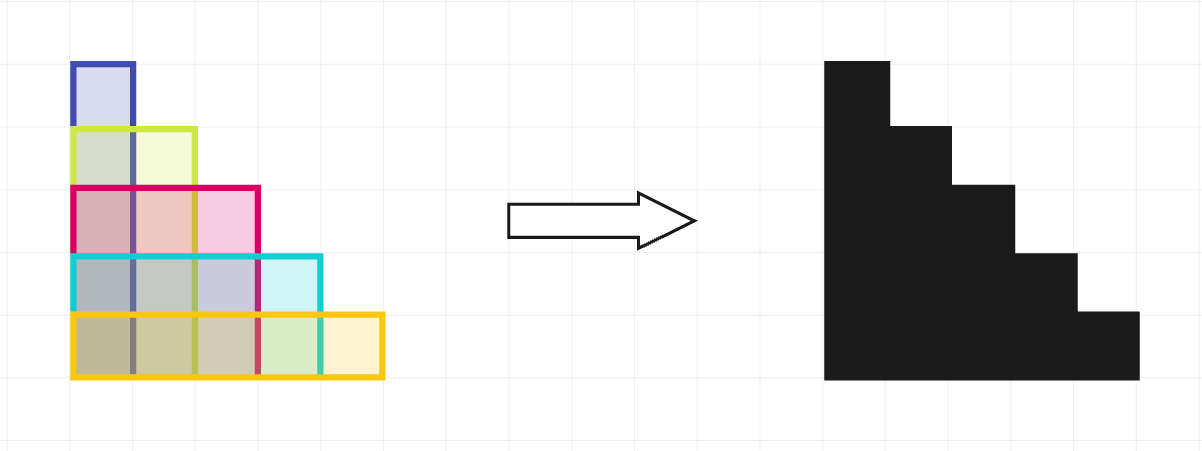
在第一个测试用例中，印章可以如左图所示使用。每个印章用不同颜色高亮显示以便区分。  所有印章都使用后，只有一个黑色区域（如右图所示），其周长为 $20$。可以证明，没有其他使用印章的方法能得到更小的总周长。 在第二个测试用例中，第二个和第三个印章可以完全放在第一个印章内部，因此最小周长等于 $8$。 由 ChatGPT 4.1 翻译