CF2031E Penchick and Chloe's Trees

离 Penchick 和 Chloe 前往新加坡的时间只剩下几个小时了，他们迫不及待地想去看看新加坡植物园的参天大树！为了抑制激动的心情，Penchick 制作了一棵有根树，让 Chloe 和他自己忙个不停。 Penchick 有一棵**有根树**，由 $n$ 个节点组成，编号从 $1$ 到 $n$，节点 $1$ 是根，Chloe 可以选择一个非负整数 $d$ 来创建一棵深度为 $d$ 的**满二叉树**。 由于 Penchick 和 Chloe 是好朋友，Chloe 希望自己的树与 Penchick 的树**同构**。为了满足这个条件，Chloe 可以在自己的树上执行以下操作，次数不限： + 选择边 $(u,v)$，其中 $u$ 是 $v$ 的父亲。 + 删除顶点 $v$ 和所有连接到 $v$ 的边，然后将 $v$ 之前的所有子节点直接连接到 $u$。 具体来说，在 $v$ 为叶子的边 $(u,v)$ 上进行操作，可以删除顶点 $v$，而不会添加任何新的边。 由于构建满二叉树非常耗时，Chloe 希望选择最小值 $d$，这样深度为 $d$ 的满二叉树就可以通过上述操作与 Penchick 的树同构。注意，她不能改变树的根。 **有根树**：树是没有环的连通图。有根树是指有一个节点是特殊的，叫做根。节点 $v$ 的父节点是从 $v$ 到根的简单路径上的第一个节点。根没有父节点。节点 $v$ 的子节点是以 $v$ 为父节点的任意节点 $u$。叶是任何没有子节点的节点。 **满二叉树**：一棵 Full Binary Tree 是有根树，其中每个节点都有 $0$ 或 $2$ 个子节点。满二叉树是指每个叶子与根的距离都相同的 Full Binary Tree。树的深度就是树根到树叶的距离。 **同构**：如果存在顶点的排列 $p$，使得当且仅当边 $(p_u,p_v)$ 存在于第二棵树中时，边 $(u,v)$ 存在于第一棵树中，并且 $p_{r_1}=r_2$。则两棵根分别为 $r_1,r_2$ 的树被认为是同构的。

本题有多组测试数据。 第一行包含测试数据的数量 $t(1\le t\le10^5)$。每组测试数据说明如下。 每组测试数据的第一行都包含一个整数 $n(2\le n\le10^6)$，表示 Penchick 的树的节点数。 每组测试数据的第二行包含 $n-1$ 个整数 $p_2,p_3,\cdots,p_n(1\le p_i\le i-1)$，表示节点 $i$ 的父节点。 保证所有测试数据中 $n$ 的总和不超过 $10^6$。

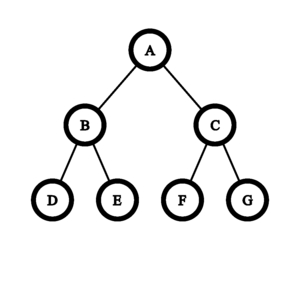
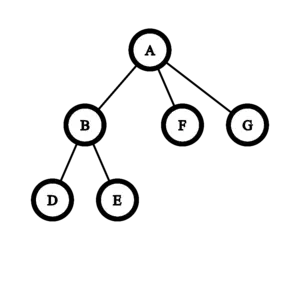
对于每个测试用例，每行输出一个整数：Chloe 的满二叉树的最小深度。 ### 样例 1 解释 对于第一个测试用例，创建一棵深度为 $2$ 的满二叉树。  考虑对边 $AC$ 进行操作。然后删除边 $AC$、$CF$ 和 $CG$ 并添加边 $AF$ 和 $AG$。 生成的树与输入的树同构。可以证明，在任何一棵深度小于 $2$ 的二叉树上进行的任何操作序列都不会导致一棵与输入所给树同构的树。  在第二个测试案例中，树已经与深度为 $3$ 的完美二叉树同构。 translated by @[chaynflow](https://www.luogu.com.cn/user/559665).

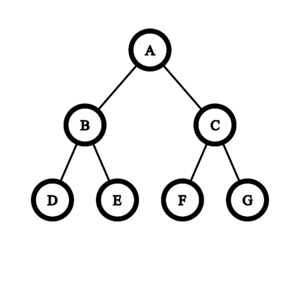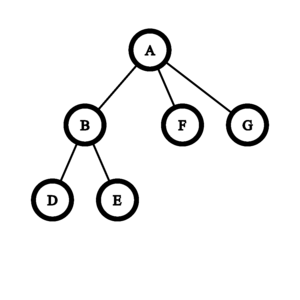For the first test case, create a perfect binary tree with depth $ 2 $ . Consider carrying out the operation on edge $ AC $ . Then the edges $ AC $ , $ CF $ , and $ CG $ are removed, and edges $ AF $ and $ AG $ are added. The resulting tree is isomorphic to the tree given in the input. It can be proven that no sequence of operations carried out on a binary tree of depth less than $ 2 $ can lead to a tree isomorphic to the tree given in the input. In the second test case, the tree is already isomorphic to a perfect binary tree of depth $ 3 $ .