CF2032D Genokraken

这是一个交互题。 在清理了水边区域后，Gretel 发现了一只名为 Genokraken 的怪物，并将其控制起来以进行科学研究。 该怪物的神经系统可以被描述为一棵有 $n$ 个节点的树 $^{\dagger}$（说真的，为什么什么都像树……），节点编号为 $0$ 到 $n-1$，其中 $0$ 号节点为根节点。 Gretel 的目标是弄清楚怪物神经系统的精确结构——更具体地说，她想知道这棵树的 $p_1, p_2, \ldots, p_{n-1}$ 的值，其中 $p_i$（$0 \le p_i < i$）表示节点 $i$ 的直接父节点（$1 \le i \le n-1$）。 她并不知道节点的具体分布，但她知道以下几个方便的事实： - 如果我们移除根节点 $0$ 及其所有相邻的边，这棵树会变成一个仅由若干条路径 $^{\ddagger}$ 组成的森林。每个最初与节点 $0$ 相邻的节点将会成为某条路径的端点。 - 节点的编号方式满足：如果 $1 \le x \le y \le n-1$，则 $p_x \le p_y$。 - 节点 $1$ 恰好有两个相邻节点（包括节点 $0$）。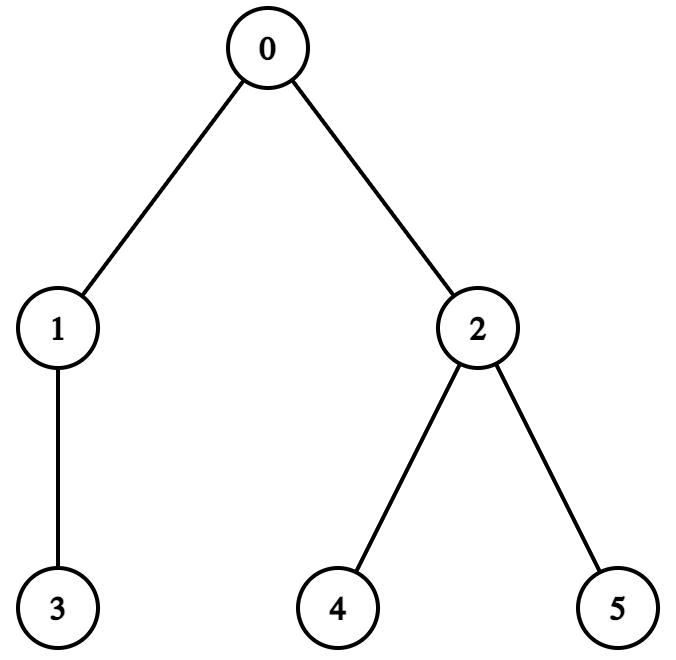    上图中的树不满足条件，因为如果移除节点 $0$，那么节点 $2$（最初与节点 $0$ 相邻）不会成为路径 $4-2-5$ 的端点。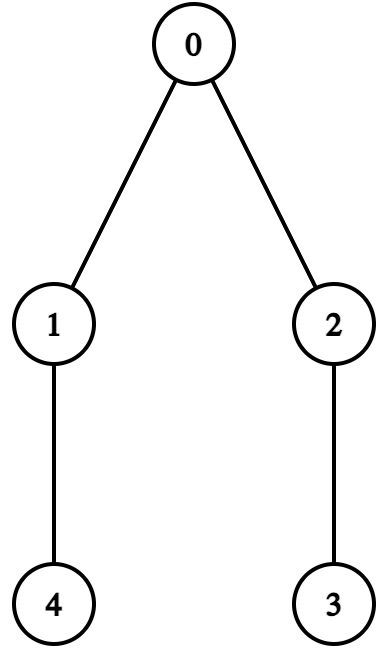 上图中的树不满足条件，因为必须满足 $p_3 \le p_4$。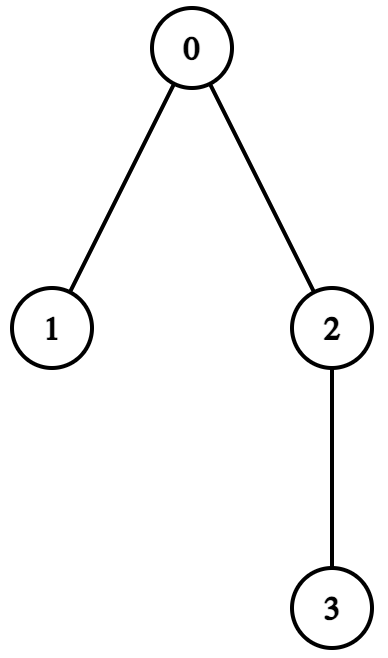 上图中的树不满足条件，因为节点 $1$ 只有一个相邻节点。 Gretel 可以向控制室发起如下查询： - "? a b"（$1 \le a, b < n$，$a \ne b$）——控制室会检查节点 $a$ 和 $b$ 之间的简单路径是否经过节点 $0$。 但为了避免过度刺激生物带来不可预知的后果，Gretel 最多只能查询 $2n-6$ 次。虽然 Gretel 很聪明，但她也不能一次做完所有事情，所以你能帮她一把吗？ $^{\dagger}$ 一棵树是一个连通图，且任意两个不同的节点之间恰好有一条简单路径。 $^{\ddagger}$ 一条路径是一棵树，其顶点可以按顺序列为 $v_1, v_2, \ldots, v_k$，边为 $(v_i, v_{i+1})$（$1 \le i < k$）。

每组测试包含多个测试用例。第一行包含一个整数 $t$（$1 \le t \le 500$）——测试用例的数量。接下来是每个测试用例的描述。 每个测试用例的第一行包含一个整数 $n$（$4 \le n \le 10^4$）——Genokraken 神经系统的节点数。 保证所有测试用例中 $n$ 的总和不超过 $10^4$。

对于每个测试用例，交互从读取整数 $n$ 开始。 然后你可以进行如下类型的查询： - "? a b"（不带引号）（$1 \le a, b < n$，$a \ne b$）。 每次查询后，读取一个整数 $r$——这是你查询的答案。你最多可以进行 $2n-6$ 次此类查询。 - 如果节点 $a$ 和 $b$ 之间的简单路径不经过节点 $0$，则 $r=0$。 - 如果节点 $a$ 和 $b$ 之间的简单路径经过节点 $0$，则 $r=1$。 - 如果你进行了超过 $2n-6$ 次查询或查询不合法，则会得到 $r=-1$。此时你需要立即终止程序，否则会得到“Wrong answer”判定。否则，你的程序会继续从已关闭的流中读取，结果不可预期。 当你确定结构后，输出一行，格式为 "! $p_1\ p_2\ \ldots\ p_{n-1}$"（不带引号），其中 $p_i$（$0 \le p_i < i$）表示节点 $i$ 的直接父节点的编号。此输出不计入 $2n-6$ 次查询限制。 每解决一个测试用例，程序应立即进入下一个测试用例。所有测试用例解决完毕后，程序应立即终止。 每次输出查询后不要忘记输出换行并刷新输出缓冲区，否则会因“Idleness limit exceeded”而判题失败。可使用如下方法刷新输出缓冲区： - C++：fflush(stdout) 或 cout.flush() - Java：System.out.flush() - Pascal：flush(output) - Python：stdout.flush() - 其它语言请查阅相关文档。 交互器是非自适应的。树的结构在交互过程中不会改变。 Hack 格式 Hack 时请使用如下格式： 第一行包含一个整数 $t$（$1 \le t \le 500$）——测试用例数量。接下来是每个测试用例的描述。 每个测试用例的第一行包含一个整数 $n$（$4 \le n \le 10^4$）——Genokraken 神经系统的节点数。 每个测试用例的第二行包含 $n-1$ 个整数 $p_1, p_2, \ldots, p_{n-1}$（$0 \le p_1 \le p_2 \le \ldots \le p_{n-1} \le n-2$，$0 \le p_i < i$）——分别表示节点 $1, 2, \ldots, n-1$ 的直接父节点编号。 每个测试用例中的 $p_1, p_2, \ldots, p_{n-1}$ 必须保证： - 如果移除根节点 $0$ 及其所有相邻的边，这棵树会变成仅由若干条路径组成的森林。每个最初与节点 $0$ 相邻的节点将会成为某条路径的端点。 - 节点 $1$ 恰好有两个相邻节点（包括节点 $0$）。 所有测试用例中 $n$ 的总和不超过 $10^4$。

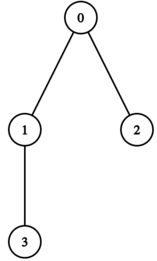
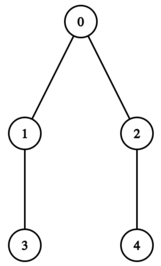
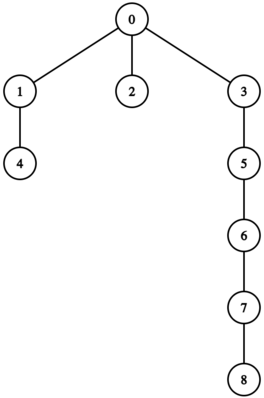
在第一个测试用例中，Genokraken 的神经系统形成如下树：  - 对于 "? 2 3" 的答案是 $1$。这意味着节点 $2$ 和 $3$ 之间的简单路径经过节点 $0$。 在第二个测试用例中，Genokraken 的神经系统形成如下树：  - 对于 "? 2 3" 的答案是 $1$。这意味着节点 $2$ 和 $3$ 之间的简单路径经过节点 $0$。 - 对于 "? 2 4" 的答案是 $0$。这意味着节点 $2$ 和 $4$ 之间的简单路径不经过节点 $0$。 在第三个测试用例中，Genokraken 的神经系统形成如下树：  由 ChatGPT 4.1 翻译