CF2035A Sliding

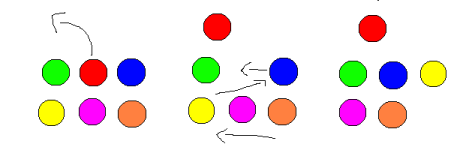
在有 $n$ 行和 $m$ 列的人群中，每个人都有一个编号，从左到右，从上到下排列。具体来说，第 $r$ 行第 $c$ 列的位置表示为 $(r, c)$，其编号为 $(r-1) \cdot m + c$。 现在，位于位置 $(r, c)$ 的人决定离开。假设这个人的编号是 $i$，那么所有编号大于 $i$ 的人会依次前移，占据编号 $j-1$ 的人的初始位置。例如：对于 $n=2$，$m=3$，$r=1$ 和 $c=2$ 的情况，如下图所示。  你的任务是计算每个受影响的人移动的曼哈顿距离之和。对于一个从位置 $(r_0, c_0)$ 移动到位置 $(r_1, c_1)$ 的人，其移动的曼哈顿距离定义为 $|r_0 - r_1| + |c_0 - c_1|$。

第一行输入一个整数 $t$（$1 \le t \le 10^4$），表示测试用例的数量。 接下来每个测试用例包含四个整数 $n$，$m$，$r$ 和 $c$（$1 \le r \le n \le 10^6$，$1 \le c \le m \le 10^6$），表示行数、列数，以及离开者的初始位置。

对于每个测试用例，输出一个整数，表示所有移动的人其曼哈顿距离之和。

- 对于第一个测试用例，编号为 $2$ 的人离开，编号为 $3$、$4$、$5$ 和 $6$ 的人需要移动，其移动距离分别为 $1$、$3$、$1$ 和 $1$。因此，答案是 $1 + 3 + 1 + 1 = 6$。 - 对于第二个测试用例，编号为 $3$ 的人离开，其后编号为 $4$ 的人移动，答案为 $1$。 **本翻译由 AI 自动生成**