CF2035A Sliding

Red was ejected. They were not the imposter. There are $ n $ rows of $ m $ people. Let the position in the $ r $ -th row and the $ c $ -th column be denoted by $ (r, c) $ . Number each person starting from $ 1 $ in row-major order, i.e., the person numbered $ (r-1)\cdot m+c $ is initially at $ (r,c) $ . The person at $ (r, c) $ decides to leave. To fill the gap, let the person who left be numbered $ i $ . Each person numbered $ j>i $ will move to the position where the person numbered $ j-1 $ is initially at. The following diagram illustrates the case where $ n=2 $ , $ m=3 $ , $ r=1 $ , and $ c=2 $ . 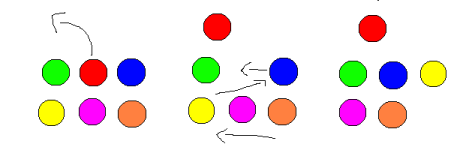Calculate the sum of the Manhattan distances of each person's movement. If a person was initially at $ (r_0, c_0) $ and then moved to $ (r_1, c_1) $ , the Manhattan distance is $ |r_0-r_1|+|c_0-c_1| $ .

The first line contains a single integer $ t $ ( $ 1\le t\le 10^4 $ ) — the number of test cases. The only line of each testcase contains $ 4 $ integers $ n $ , $ m $ , $ r $ , and $ c $ ( $ 1\le r\le n\le 10^6 $ , $ 1 \le c \le m \le 10^6 $ ), where $ n $ is the number of rows, $ m $ is the number of columns, and $ (r,c) $ is the position where the person who left is initially at.

For each test case, output a single integer denoting the sum of the Manhattan distances.

For the first test case, the person numbered $ 2 $ leaves, and the distances of the movements of the person numbered $ 3 $ , $ 4 $ , $ 5 $ , and $ 6 $ are $ 1 $ , $ 3 $ , $ 1 $ , and $ 1 $ , respectively. So the answer is $ 1+3+1+1=6 $ . For the second test case, the person numbered $ 3 $ leaves, and the person numbered $ 4 $ moves. The answer is $ 1 $ .