CF2038E Barrels
题目描述
假设你拥有 $n$ 个水桶,它们依次排放,编号为 $1$ 到 $n$。
每个水桶是相同的,底面积为一个单位,因此水桶内的水量对应水柱的高度。起初,第 $i$ 个水桶中含有 $v_i$ 单位的水。
相邻的水桶之间通过管道相连。具体来说,对于每个从 $1$ 到 $n-1$ 的 $i$,水桶 $i$ 与水桶 $i+1$ 通过一个高度为 $h_i$ 的水平管道相连。管道的宽度可以忽略不计。这些管道可以让水在水桶之间流动。
现在,你想对这些水桶进行操作。你的目标是通过向水桶中投放粘土来最大化第一个水桶中的水量。每一步,你可以选择任意一个水桶,向其中添加一单位的粘土。粘土的单位体积与水相同,但粘土比水重且不会与水混合,因此它会下沉并均匀分布在桶底。
由于粘土具有黏性,当粘土的高度足够时,它会封住管道。更确切地说,如果管道的高度为 $h$,当粘土的高度达到或低于 $h$ 时,管道仍然能正常工作。然而,一旦你向水桶中多加了一单位的粘土,管道就会立刻被封住,阻止水在水桶之间流动。
你拥有大量的粘土,因此可以多次执行上述操作。但在每次操作之后,你需要等待水达到新的平衡状态。
你能让第一个水桶中的水量达到的最大值是多少?
假定水桶足够高,因此不会溢出,并且可以忽略管道的宽度。
输入格式
第一行包含一个整数 $n$($2 \le n \le 2 \cdot 10^5$),表示水桶的数量。
第二行包含 $n$ 个整数 $v_1, v_2, \dots, v_n$($0 \le v_i \le 10^6$),表示每个水桶的初始水量。
第三行包含 $n - 1$ 个整数 $h_1, h_2, \dots, h_{n - 1}$($1 \le h_i \le 10^6$),表示水桶之间的管道高度。
请注意,输入数据保证水最初处于平衡状态。
输出格式
输出一个数字,表示第一个水桶中可能达到的最大水量。你的答案将被认为是正确的,如果其绝对误差或相对误差不超过 $10^{-6}$。
格式上,设你的答案为 $a$,标准答案为 $b$。当且仅当 $\frac{|a - b|}{\max{(1, |b|)}} \le 10^{-6}$ 时,答案被接受。
**本翻译由 AI 自动生成**
说明/提示
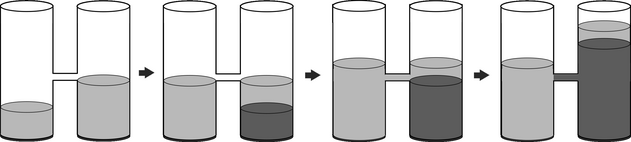
An optimal strategy for the first example is shown in the picture below: