CF2038K Grid Walk

You have an $ n \times n $ grid and two integers $ a $ and $ b $ . Both the rows and the columns are numbered from $ 1 $ to $ n $ . Let's denote the cell at the intersection of the $ i $ -th row and the $ j $ -th column as $ (i, j) $ . You are standing in the cell $ (1, 1) $ and want to move into the cell $ (n, n) $ . Suppose you are in the cell $ (i, j) $ ; in one step, you can move either into the cell $ (i, j + 1) $ or into the cell $ (i + 1, j) $ if the corresponding cells exist. Let's define the cost of the cell $ (i, j) $ as $ c(i, j) = \gcd(i, a) + \gcd(j, b) $ (here, $ \gcd(x,y) $ denotes the greatest common divisor of $ x $ and $ y $ ). The cost of the route from $ (1, 1) $ to $ (n, n) $ is the sum of costs of the visited cells (including the starting cell and the finishing cell). 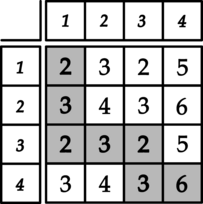Find the route with minimum possible cost and print its cost.

The only line contains three integers $ n $ , $ a $ , and $ b $ ( $ 2 \le n \le 10^6 $ ; $ 1 \le a, b \le 10^6 $ ).

Print one integer — the cost of the cheapest route from $ (1, 1) $ to $ (n, n) $ .

The first example is described in the picture above.