CF203D Hit Ball

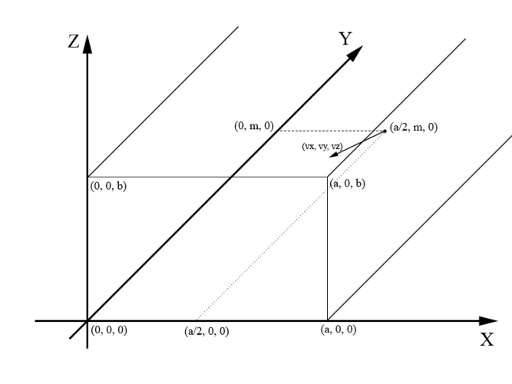
瓦莱拉在体育场踢足球时，突然天降大雨。他躲进了看台下的走廊，躲避雨水。然而，他对足球的热爱丝毫未减，于是决定在走廊里练习踢球。在离门距离足够远的地方，他放好球并用力踢了出去。球在墙壁、天花板和地板上四处反弹，最后撞在了出口的门上。由于球是湿的，在门上留下了一个印记。瓦莱拉现在想确切地知道这个印记的位置。 我们可以将这个情景抽象化为一个几何模型。球可以被看作是空间中的一个点。走廊的门是一个位于平面 $xOz$ 上的矩形，其中左下角位于点 $(0,0,0)$，右上角位于点 $(a,0,b)$。走廊本身是一个垂直于 $y$ 轴无限延伸的长方体。在走廊中，地板是平面 $xOy$，而天花板则是一个平行于 $xOy$ 的平面，经过点 $(a,0,b)$。同样，一面墙是平面 $yOz$，另一面墙与此平面平行，经过点 $(a,0,b)$。 当球的 $y$ 坐标为 $0$ 时，我们称之为球撞到了门。因此，印记的坐标是 $(x_{0}, 0, z_{0})$，其中 $0 \le x_{0} \le a$ 且 $0 \le z_{0} \le b$。为了踢出球，瓦莱拉在距离门 $m$ 的位置将球放置在走廊中心点 $\left(\frac{a}{2}, m, \frac{b}{2}\right)$。击球后，球以速度 $(v_{x}, v_{y}, v_{z})$ 移动。也就是说，如果球当前在 $(x, y, z)$ 位置，那么一秒钟后它将移动到 $(x+v_{x}, y+v_{y}, z+v_{z})$。 请参考注释中的图像以获得更清晰的理解。 球在撞到天花板、地板或走廊墙壁时，会根据反射定律（入射角等于反射角）进行反弹。在这个问题中，我们运用了理想物理模型，也就是说不考虑空气阻力、摩擦力或能量损失。

第一行输入三个用空格分隔的整数 $a, b, m$，其中 $1 \le a, b, m \le 100$。前两个整数定义了天花板和走廊墙面经过的点 $(a,0,b)$。第三个整数 $m$ 表示瓦莱拉离门的距离。 第二行包括三个用空格分隔的整数 $v_{x}, v_{y}, v_{z}$，其中 $|v_{x}|, |v_{y}|, |v_{z}| \le 100$，并且 $v_{y} < 0, v_{z} \ge 0$，表示击球后的球速。 从题目保证，球一定会撞到门。

输出两个实数 $x_{0}, z_{0}$，表示球撞到出口门时的位置坐标 $(x_{0}, 0, z_{0})$。答案的绝对误差或相对误差须不超过 $10^{-6}$，方为有效。 **本翻译由 AI 自动生成**