CF2040B Paint a Strip
题目描述
你有一个长度为 $n$ 的数组 $a_1, a_2, \ldots, a_n$,其元素全为零。
可以对该数组进行两种操作:
1. 选择一个下标 $i$(满足 $1 \le i \le n$ 且 $a_i = 0$),将 $a_i$ 设为 $1$;
2. 选择一对下标 $l$ 和 $r$(满足 $1 \le l \le r \le n$、$a_l = 1$、$a_r = 1$ 且 $a_l + \ldots + a_r \ge \lceil\frac{r - l + 1}{2}\rceil$),将区间 $[l, r]$ 中所有元素设为 $1$。
你的任务是计算,使数组中所有元素都变为 $1$,至少需要多少次第一种操作?
输入格式
输入包含多组测试用例。第一行是整数 $t$($1 \le t \le 10^4$),表示测试用例的数量。接下来每个测试用例用一行表示,包含一个整数 $n$($1 \le n \le 10^5$),表示数组的长度。
需要注意,所有测试用例中 $n$ 的总和没有限制。
输出格式
对于每组测试用例,输出一个整数,表示完成任务所需的最少第一种操作次数。
说明/提示
- 对于第一个测试用例,你可以对 $i = 1$ 操作一次即可。
- 对于第二个测试用例,可以按以下步骤操作:
1. 对 $i = 1$ 进行第一种操作,数组变为 $[1, 0]$。
2. 对 $i = 2$ 进行第一种操作,数组变为 $[1, 1]$。
第二个测试用例的操作步骤如下图所示: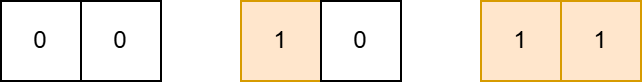
- 对于第三个测试用例,可以按以下步骤操作:
1. 对 $i = 1$ 进行第一种操作,数组变为 $[1, 0, 0, 0]$。
2. 对 $i = 4$ 进行第一种操作,数组变为 $[1, 0, 0, 1]$。
3. 对 $l = 1$ 和 $r = 4$ 进行第二种操作,因为 $a_1 + a_2 + a_3 + a_4 = 2$,满足不小于 $\lceil\frac{r - l + 1}{2}\rceil = 2$,所以可以将区间内元素设为 $1$,数组变为 $[1, 1, 1, 1]$。
第三个测试用例的操作步骤如下图所示: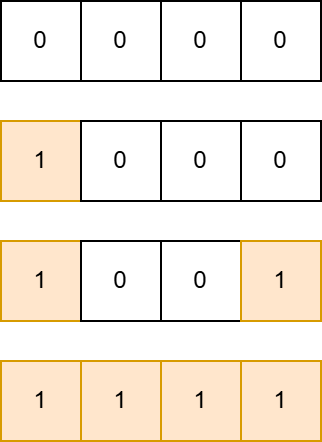
**本翻译由 AI 自动生成**