CF2040D Non Prime Tree

给你一棵拥有 $n$ 个顶点的树。 你的任务是构造一个包含 $n$ 个不同整数的数组，这些整数从 $1$ 到 $2 \cdot n$ 分别取值。同时要求对于树中的任意一条边 $u_i \leftrightarrow v_i$，对应的数组元素差值 $|a_{u_i} - a_{v_i}|$ 不是质数。 请你找出任意一个符合以上条件的数组，如果不存在这样的数组，请输出 $-1$。

每组测试用例包含多个测试。首行给出测试用例数量 $t$（$1 \le t \le 10^4$）。每个测试用例的描述如下： 第一行一个整数 $n$（$2 \le n \le 2 \cdot 10^5$），表示树的顶点数量。 接下来的 $n-1$ 行，每行描述一条树的边。具体来说，第 $i$ 行给出两个整数 $u_i$ 和 $v_i$（$1 \le u_i, v_i \le n$；$u_i \neq v_i$），表示节点 $u_i$ 和 $v_i$ 之间有边相连。 可以保证给定的边组成一棵树。此外，所有测试用例中的 $n$ 总和不超过 $2 \cdot 10^5$。

对于每个测试用例，如果找到满足条件的数组，输出该数组的元素 $a_1, a_2, \ldots, a_n$。如果找不到，则输出 $-1$。

如下图所示的答案中，用对应数组 $a$ 的元素替代了顶点编号： 第一组数据的树结构 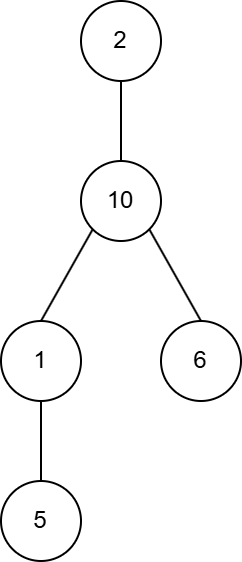 第二组数据的树结构 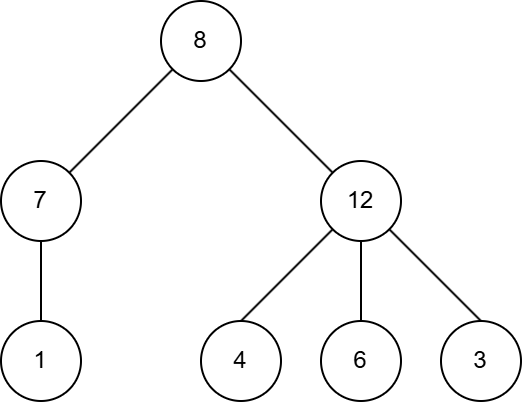 **本翻译由 AI 自动生成**