CF2040E Control of Randomness

You are given a tree with $ n $ vertices. Let's place a robot in some vertex $ v \ne 1 $ , and suppose we initially have $ p $ coins. Consider the following process, where in the $ i $ -th step (starting from $ i = 1 $ ): - If $ i $ is odd, the robot moves to an adjacent vertex in the direction of vertex $ 1 $ ; - Else, $ i $ is even. You can either pay one coin (if there are some left) and then the robot moves to an adjacent vertex in the direction of vertex $ 1 $ , or not pay, and then the robot moves to an adjacent vertex chosen uniformly at random. The process stops as soon as the robot reaches vertex $ 1 $ . Let $ f(v, p) $ be the minimum possible expected number of steps in the process above if we spend our coins optimally. Answer $ q $ queries, in the $ i $ -th of which you have to find the value of $ f(v_i, p_i) $ , modulo $ ^{\text{∗}} $ $ 998\,244\,353 $ . $ ^{\text{∗}} $ Formally, let $ M = 998\,244\,353 $ . It can be shown that the answer can be expressed as an irreducible fraction $ \frac{p}{q} $ , where $ p $ and $ q $ are integers and $ q \not \equiv 0 \pmod{M} $ . Output the integer equal to $ p \cdot q^{-1} \bmod M $ . In other words, output such an integer $ x $ that $ 0 \le x < M $ and $ x \cdot q \equiv p \pmod{M} $ .

Each test contains multiple test cases. The first line contains the number of test cases $ t $ ( $ 1 \le t \le 10^3 $ ). The description of the test cases follows. The first line of each test case contains two integers $ n $ and $ q $ ( $ 2 \le n \le 2 \cdot 10^3 $ ; $ 1 \le q \le 2 \cdot 10^3 $ ) — the number of vertices in the tree and the number of queries. The next $ n - 1 $ lines contain the edges of the tree, one edge per line. The $ i $ -th line contains two integers $ u_i $ and $ v_i $ ( $ 1 \le u_i, v_i \le n $ ; $ u_i \neq v_i $ ), denoting the edge between the nodes $ u_i $ and $ v_i $ . The next $ q $ lines contain two integers $ v_i $ and $ p_i $ ( $ 2 \le v_i \le n $ ; $ 0 \le p_i \le n $ ). It's guaranteed that the given edges form a tree. It is guaranteed that the sum of $ n $ over all test cases does not exceed $ 2 \cdot 10 ^ 3 $ . It is guaranteed that the sum of $ q $ over all test cases does not exceed $ 2 \cdot 10 ^ 3 $ .

For each test case, print $ q $ integers: the values of $ f(v_i, p_i) $ modulo $ 998\,244\,353 $ . Formally, let $ M = 998\,244\,353 $ . It can be shown that the answer can be expressed as an irreducible fraction $ \frac{p}{q} $ , where $ p $ and $ q $ are integers and $ q \not \equiv 0 \pmod{M} $ . Output the integer equal to $ p \cdot q^{-1} \bmod M $ . In other words, output such an integer $ x $ that $ 0 \le x < M $ and $ x \cdot q \equiv p \pmod{M} $ .

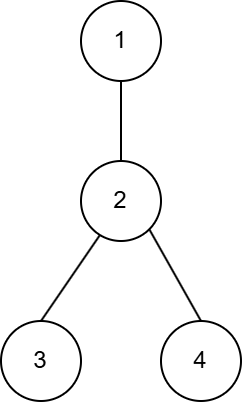The tree in the first test case: In the first query, the expected value is equal to $ 1 $ , since the robot starts moving from vertex $ 2 $ to vertex $ 1 $ in the first step and the process stops. Let's calculate the expected value in the second query ( $ x $ is the number of steps): - $ P(x < 2) = 0 $ , the distance to vertex $ 1 $ is $ 2 $ and the robot cannot reach it in fewer steps. - $ P(x = 2) = \frac{1}{3} $ , since there is only one sequence of steps leading to $ x = 2 $ . This is $ 3 \rightarrow_{1} 2 \rightarrow_{0.33} 1 $ with probability $ 1 \cdot \frac{1}{3} $ . - $ P(x \bmod 2 = 1) = 0 $ , since the robot can reach vertex $ 1 $ by only taking an even number of steps. - $ P(x = 4) = \frac{2}{9} $ : possible paths $ 3 \rightarrow_{1} 2 \rightarrow_{0.67} [3, 4] \rightarrow_{1} 2 \rightarrow_{0.33} 1 $ . - $ P(x = 6) = \frac{4}{27} $ : possible paths $ 3 \rightarrow_{1} 2 \rightarrow_{0.67} [3, 4] \rightarrow_{1} 2 \rightarrow_{0.67} [3, 4] \rightarrow_{1} 2 \rightarrow_{0.33} 1 $ . - $ P(x = i \cdot 2) = \frac{2^{i - 1}}{3^i} $ in the general case. As a result, $ f(v, p) = \sum\limits_{i=1}^{\infty}{i \cdot 2 \cdot \frac{2^{i - 1}}{3^i}} = 6 $ . 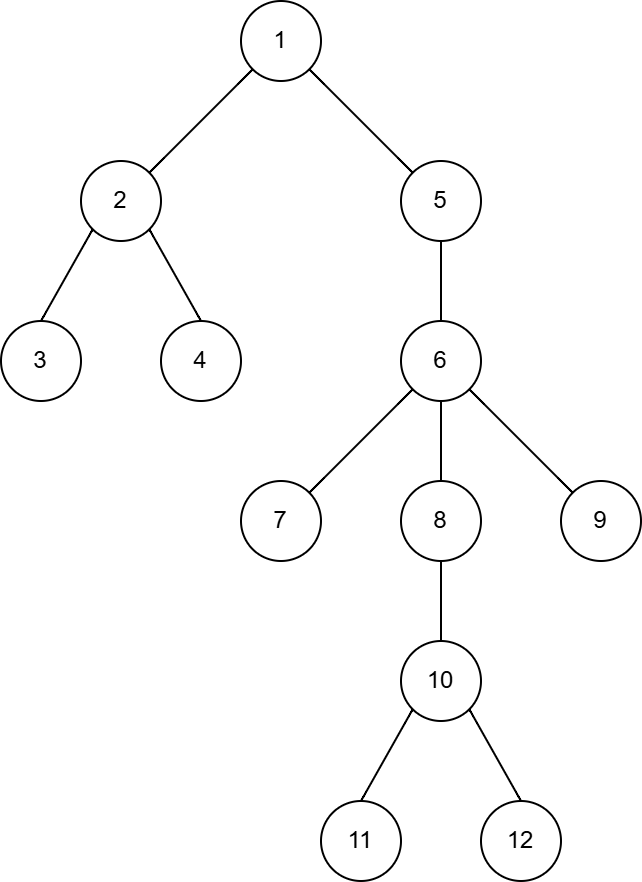The tree in the second test case: