CF2040F Number of Cubes

Consider a rectangular parallelepiped with sides $ a $ , $ b $ , and $ c $ , that consists of unit cubes of $ k $ different colors. We can apply cyclic shifts to the parallelepiped in any of the three directions any number of times $ ^{\text{∗}} $ . There are $ d_i $ cubes of the $ i $ -th color ( $ 1 \le i \le k $ ). How many different parallelepipeds (with the given sides) can be formed from these cubes, no two of which can be made equal by some combination of cyclic shifts? 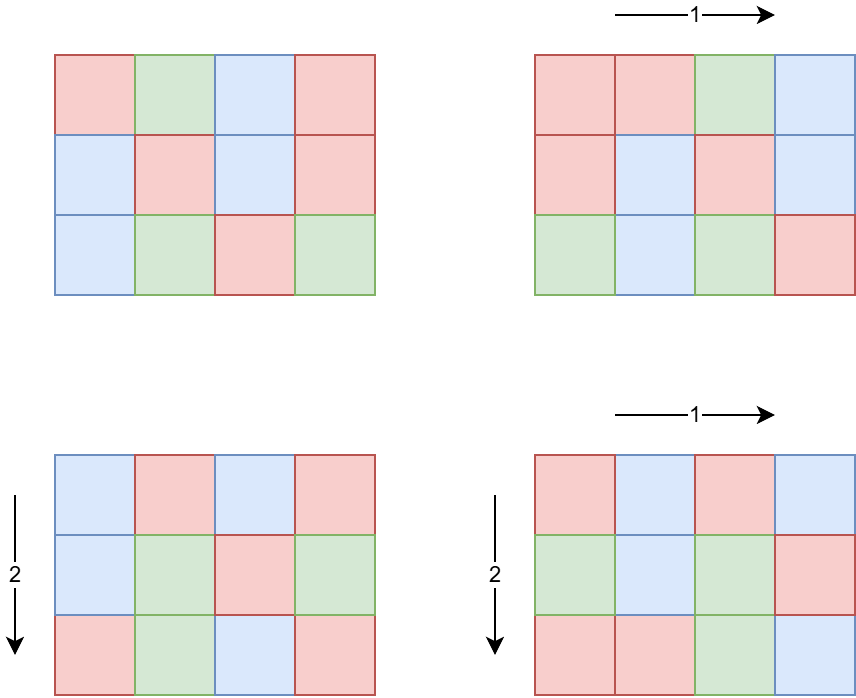$ ^{\text{∗}} $ On the image: - Top left shows the top view of the original parallelepiped. Lower layers will shift in the same way as the top layer. - Top right shows the top view of a parallelepiped shifted to the right by $ 1 $ . - Bottom left shows the top view of a parallelepiped shifted down by $ 2 $ . - Bottom right shows the top view of a parallelepiped shifted to the right by $ 1 $ and down by $ 2 $ . 

Each test contains multiple test cases. The first line contains the number of test cases $ t $ ( $ 1 \le t \le 100 $ ). The description of the test cases follows. The first line of each test case contains four integers: $ a $ , $ b $ , $ c $ , and $ k $ ( $ 1 \le a, b, c \le 3 \cdot 10^6 $ ; $ a \cdot b \cdot c \le 3 \cdot 10^6 $ ; $ 1 \le k \le 10^6 $ ) — three sides of the parallelepiped and the number of colors of unit cubes. The second line of each test case contains $ k $ integers $ d_1, d_2, \ldots, d_k $ ( $ 1 \le d_1 \le d_2 \le \ldots \le d_k \le 3 \cdot 10^6 $ ) — the elements of the array $ d $ : the number of cubes of a given color. It is guaranteed that in each test case the sum of the elements of the array $ d $ is equal to $ a \cdot b \cdot c $ . It is guaranteed that the sum of $ k $ over all test cases does not exceed $ 10 ^ 6 $ .

For each test case, print one integer — the number of different parallelepipeds modulo $ 998\,244\,353 $ .

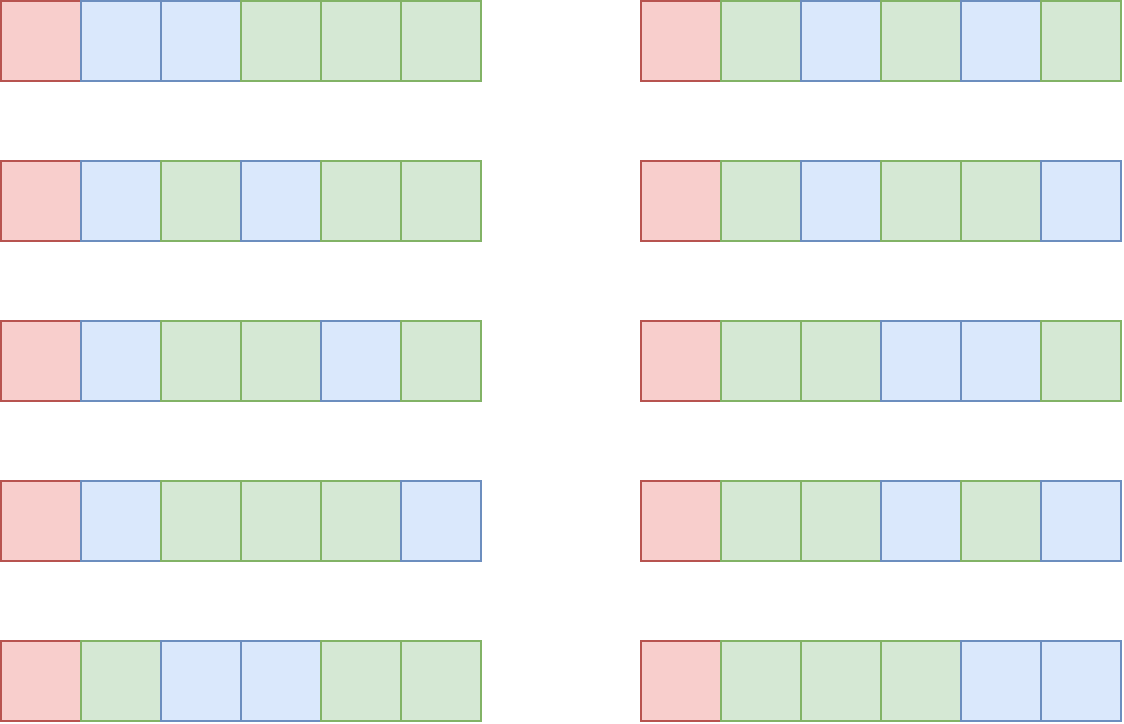
In the first test case, there is only one parallelepiped, which consists of one unit cube. Possible parallelepipeds in the second test case