CF2040F Number of Cubes

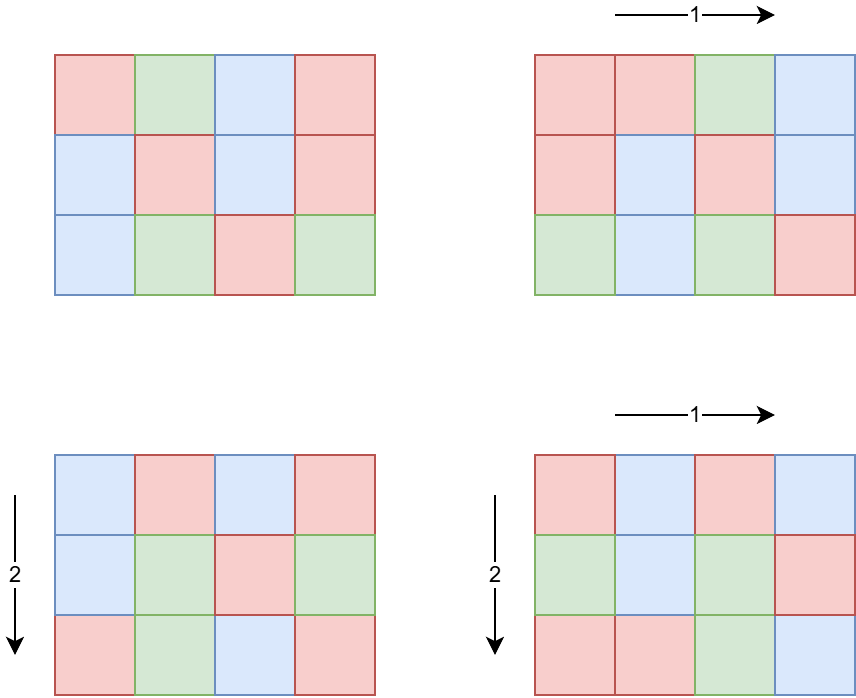
有一个长方体，其长、宽、高分别为 $a$、$b$ 和 $c$，由 $k$ 种不同颜色的单位立方体填充组成。我们可以对这个长方体在任意三个方向执行任意次数的循环移位 $^{\text{∗}}$。 其中，第 $i$ 种颜色的单位立方体数量为 $d_i$（其中 $1 \le i \le k$）。请问：用这些立方体可以拼成多少种不同的长方体结构，使得没有哪两种结构可以通过任意组合的循环移位变得相同？ $^{\text{∗}}$ 如图所示： - 左上角是原始长方体的俯视图（下层与顶层保持同样的移动方式）。 - 右上角是向右移动 $1$ 格后的长方体俯视图。 - 左下角是向下移动 $2$ 格后的长方体俯视图。 - 右下角是分别向右移动 $1$ 格并向下移动 $2$ 格后的长方体俯视图。 

第一个输入为测试用例的数量 $t$（$1 \le t \le 100$）。接下来是每个测试用例的详细描述。 每个测试用例的第一行包含四个整数：$a$、$b$、$c$ 和 $k$（其中 $1 \le a, b, c \le 3 \cdot 10^6$；$a \cdot b \cdot c \le 3 \cdot 10^6$；$1 \le k \le 10^6$），表示组成长方体的三条边长及单位立方体的颜色数。 每个测试用例的第二行包含 $k$ 个整数：$d_1, d_2, \ldots, d_k$（其中 $1 \le d_1 \le d_2 \le \ldots \le d_k \le 3 \cdot 10^6$），代表每种颜色的立方体个数。 保证在每个测试用例中，所有 $d$ 数组元素的和等于 $a \cdot b \cdot c$。 保证所有测试用例中，各颜色总数 $k$ 的和不超过 $10^6$。

对于每个测试用例，输出一个整数，表示不同长方体的数量对 $998\,244\,353$ 取模后的结果。

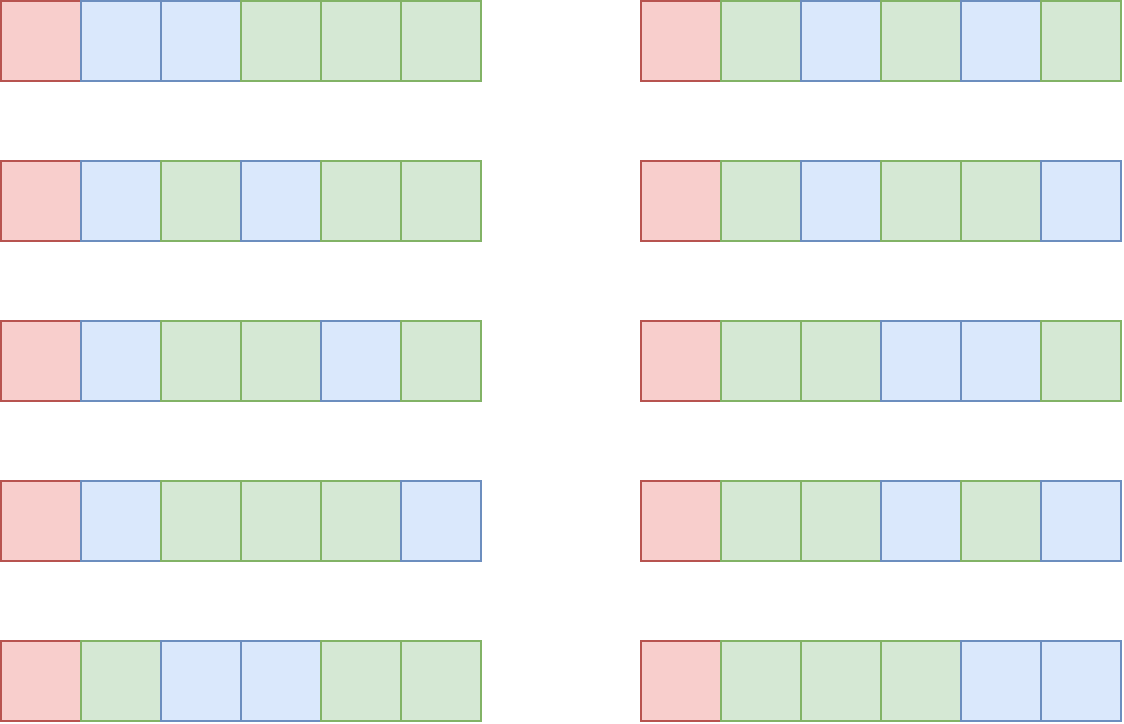
在第一个测试用例中，只有一个由一个单位立方体组成的长方体。 第二个测试用例中可能构成的长方体如图所示：  **本翻译由 AI 自动生成**