CF2041F Segmentation Folds

Peter 喜欢折线段玩。有一条线段位于数轴上的区间 $[\ell, r]$。现如今正是折叠线段的好时机，Peter 决定小心翼翼地对这条线段进行折叠。每次操作中，他可以选择以下两种方式之一（在可能的情况下）： 1. 操作 $\tt{LTR}$：他从左向右折线段，使得左端点 $\ell$ 与某个点 $x$ 重合（$\ell < x \le r$），并且 $\ell + x$ 是质数。当他选择此操作时，总是选取最大的 $x$ 值。折叠后，线段所在的区间变为 $[\frac{1}{2}(\ell + x), r]$。 2. 操作 $\tt{RTL}$：他从右向左折线段，使得右端点 $r$ 与某个点 $x$ 重合（$\ell \le x < r$），并且 $r + x$ 是质数。当他选择此操作时，总是选取最小的 $x$ 值。折叠后，线段所在的区间变为 $[\ell, \frac{1}{2}(r + x)]$。 一个折叠序列是指这两种操作的组合。Peter 想要通过多次折叠，使线段的长度尽可能短，且无法再缩短。区间的长度自然定义为 $r - \ell$。考虑以下例子：假设我们折叠一段初始为 $[1, 30]$ 的线段。有三种折叠方式能使最终区间长度最短，如下图所示。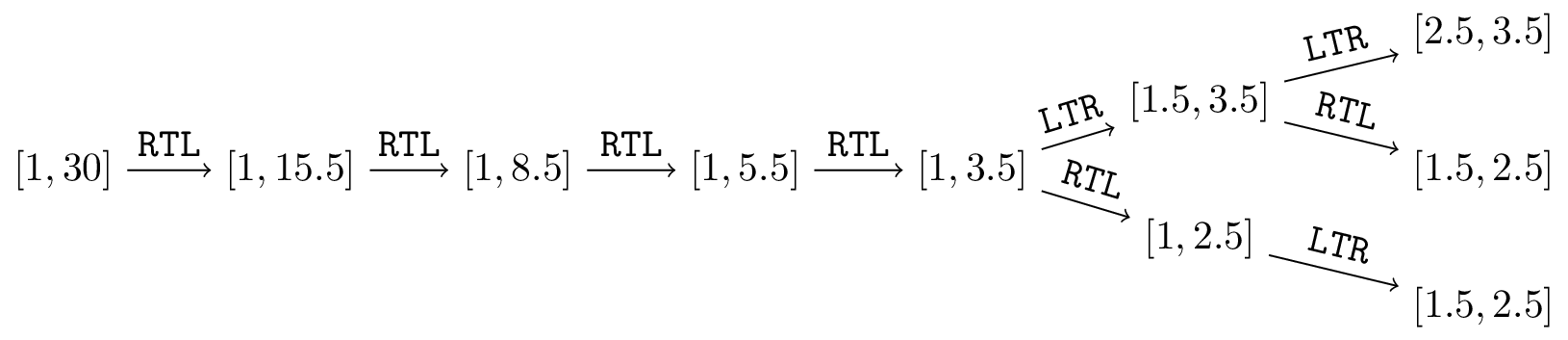  请你帮助 Peter 确定有多少种不同的折叠序列可以使线段达到最短长度。结果需要对 $998244353$ 取模。 注：一个大于 $1$ 的整数 $p$ 是质数，当且仅当不存在整数 $a, b > 1$ 使得 $p = ab$。

第一行包含一个整数 $t$，表示测试用例的数量。接下来的 $t$ 行中，每行包含两个整数 $\ell$ 和 $r$。 - $1 \le t \le 10$ - $1 \le \ell < r \le 10^{12}$ - $r - \ell \le 10^5$

对于每个测试用例，输出一行，表示能将给定线段折叠到最短长度的折叠序列数量，结果对 $998244353$ 取模。 **本翻译由 AI 自动生成**