CF2041G Grid Game

Claire 喜欢画线。她拿到一张 $ n \times n $ 的网格纸，并开始在上面画所谓的「线」。不过，Claire 所说的「线」并不是我们通常意义上的，而是指一组连续的竖直网格单元格。当她画这样的「线」时，这些单元格会被涂黑。最初，所有单元格都是白色的，画线会将其中的一些变成黑色。画了几条线后，Claire 想知道：她可以将多少个额外的白色单元格涂黑，以确保剩下的白色单元格不再形成一个单一连通块。 在网格中，两个单元格直接相连是指它们共享一个边。如果两个单元格 $ x $ 和 $ y $ 间接相连，说明存在一个单元格序列 $ c_0, c_1, \ldots, c_k $ ，且 $ k > 1 $ ，使得 $ c_0 = x $ ，$ c_k = y $ ，并且对于每个 $ i \in \{1, 2, \ldots, k\} $ ，单元格 $ c_i $ 和 $ c_{i-1} $ 是直接相连的。如果一组单元格中任意两个单元格都是直接或间接相连的，那么它们就形成一个连通块。 网格有 $ n $ 行和 $ n $ 列，编号从 $ 1 $ 到 $ n $ 。Claire 将在上面画 $ q $ 条线。第 $ i $ 条线在 $ y_i $ 列上，从 $ s_i $ 行画到 $ f_i $ 行，每个 $ i \in \{1, 2, \ldots, q\} $ 都满足 $ s_i \leq f_i $ 。注意，每一条被线通过的单元格都会被涂黑。下图展示了一个 $ 20 \times 20 $ 的网格，在其中画了 $ q = 67 $ 条线。标记为红色星号的单元格表示，如果 Claire 将这些单元格涂黑，那么所有的白色单元格将不再形成一个连通的整体。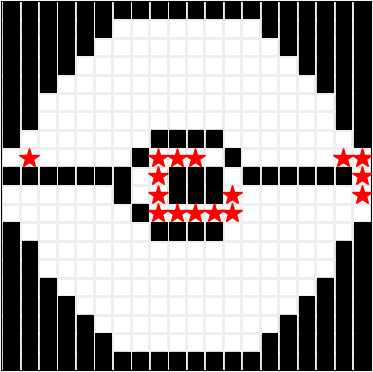  可以假设，在画完 $ q $ 条线之后，剩余的白色单元格仍形成一个包含至少三个白色单元格的连通块。

第一行输入一个整数 $ t $ ，代表测试用例的数量。接下来的每一个测试用例从一行开始，这一行包含两个整数 $ n $ 和 $ q $ ，表示网格的尺寸是 $ n \times n $ ，并且 Claire 将在其上画 $ q $ 条线。接下来的 $ q $ 行中，每行包含三个整数 $ y_i $ 、$ s_i $ 和 $ f_i $ 。 - $ 1 \le t \le 125 $ - $ 2 \le n \le 10^9 $ - $ q \ge 1 $ ，所有 $ q $ 的总和不超过 $ 10^5 $ 。 - $ 1 \le y_i \le n $ - $ 1 \le s_i \le f_i \le n $ - 至少有三个白色单元格，并且所有白色单元格形成一个连通块。

输出一个整数，指示 Claire 可以选择多少种方式将额外的白色单元格涂成黑色，以便剩余的白色单元格不再组成一个单一的连通块。 **本翻译由 AI 自动生成**